انجام خدمات نرم افزار SMART PLS4

آموزش

نرم افزار SMART PLS4 را بصورت ویدیو و متن آموزش می دهیم.

اطلاعات بیشتر

مشاوره

مشاوره تخصصی برای انجام تحقیقات کیفی و کمی به شما خواهیم داد.

More info

انجام تحلیل

تحلیل آماری فصل 4 رساله و مقالات داخلی و خارجی را انجام می دهیم.

More info

تعدادی از ویژگی های موجود در SmartPLS 4

صفحات گرافیکی بروز شده و بهتر نمایش می دهد.
10 زبان برای کار وجود دارد.

در نرم افزار عملکرد بهبود یدا کرده است.

می توانیم داده ها را علاوه بر CSV از Excel یا SPSS بارگزاری کنیم.
انجام تعدیل چندگانه متغیرها(تعاملات سه جانبه)
آزمایش درون زایی با جفت گاوسی
انجام مدل‌های رگرسیون، شامل بسیاری از تشخیص‌ها و تحلیل ها و گزارش‌های مفید برای انجام کامل تحلیل‌های تحقیق
تجزیه و تحلیل داده ها ازنوع فرآیند، همچون راه‌اندازی اثرات مستقیم و غیرمستقیم شرطی
تجزیه و تحلیل شرایط ضروری (NCA) شامل آزمون معنی داری
حسابداری برای نوع مقیاس متغیرهای تحقیق در اکثر الگوریتم ها
تجزیه و تحلیل PLS-SEM استاندارد، غیر استاندارد و میانگین محور
فایل های داده جدید را بصورت مستقیم می توان از نتایج محاسبات ایجاد کرد(مفید برای مدل های مرتبه بالاتر)
تعداد زیادی از مدل های نمونه جدید در نرم افزار آمده است.

More videos on SmartPLS 4

ما کانال YouTube James Gaskin را توصیه می کنیم. او قبلاً ویدیوهای خوبی در مورد SmartPLS 4 منتشر کرده است:

01 Crafted by hand

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut condimentum, nisi at suscipit convallis, mi diam maximus odio, vitae mollis odio lorem vel diam. Nullam rutrum rhoncus euismod. Integer ornare nisl urna, eu vehicula urna sagittis ac.

02 Passionate for real

03 We promote integrity

Explore our services

Branding

Interior design

Architecture

آموزش Smart PLS4

تعدادی از ویژگی های موجود در SmartPLS 4

صفحات گرافیکی بروز شده و بهتر نمایش می دهد.
10 زبان برای کار وجود دارد.

در نرم افزار عملکرد بهبود پیدا کرده است.

آموزش Smart PLS4

در روش های پیشین تحلیل آماری،برای تعیین یا تائید فرضیه های نظری مبتنی بر تحلیل داده های تجربی،برفنون مبتنی بر رگرسیون(تحلیل رگرسیون چندگانه،تحلیل تشخیصی، تحلیل لوجستیک وتحلیل واریانس) وتحلیل عاملی یاخوشه ای،به عنوان مجموعه اصلی ازابزارهای آماری تاکید می شود.محققان رشته های مختلف،بااستفاده ازاین روش ها نتایجی به دست آورده اند تا بر اساس آن راهی برای درک جهان بیابند.ازجمله این روش ها می توان به روش تحلیل عاملی اسپیرمن(1904)درتعیین ساختارهای عاملی در روانشناسی وتحلیل خوشه ای هافستد(1983)برای کشف تفاوت های میان فرهنگی در جامعه شناسی اشاره کرد.اما در میان این روش ها سه محدودیت یکسان مشاهده می شود که عبارتنداز:

1)پیش فرض ساختارمدل ساده(حداقل در مورد رویکردهای مبتنی بر رگرسیون)،

2)پیش فرض قابل مشاهده بودن همۀ متغیرها،

3)پیش فرض اندازه گیری بدون خطای همۀ متغیرها.

بنابراین هرمتغیری که مستقیماً باهرچیز قابل مشاهده مطابقت نداشته باشد باید به عنوان غیر قابل مشاهده درنظر گرفته شود(دیجکسترا،1983).بر اساس این تعریف تنها برخی از متغیرها مانند سن و جنسیت متغیرهای قابل مشاهده تلقی می شوند،حال آن که اثر ومشخصات مولکول ها،فرایندها،ژن ها،ویروس ها وباکتری ها معمولاً به صورت غیر مستقیم مشاهده می شوند(والد،1993).درمورد این فرض که همۀ متغیرها بدون خطا اندازه گیری می شوند،باید دانست هر مشاهده ای از دنیای واقعی با خطا های اندازه گیری خاصی همراه است،که از دوبخش تشکیل می شوند(باگوزی،یی و فیلیپس،1991).نخست خطای تصادفی که از ترتیب گویه ها در پرسشنامه یا خستگی پاسخگو ناشی می شود(هیلر و رای،1972) و دوم خطای منظم،از قبیل واریانس روش(نسبت دادن واریانس به روش اندازه گیری به جای سازۀ مورد بررسی)(باگوزی و همکاران،1991).به دلیل اینکه نمره مشاهده شدۀ یک گویه از سه بخش تشکیل شده است،یعنی نمره واقعی متغیر،خطای تصادفی و خطای منظم.با دید دقیق تر می توان گفت روش های پیشین ،تنها هنگامی قابل استفاده هستند که مولفه های خطای منظم وتصادفی نداشته باشند که این امر به ندرت در واقعیت امکان پذیر است(هین لاین و کاپلان،2004).

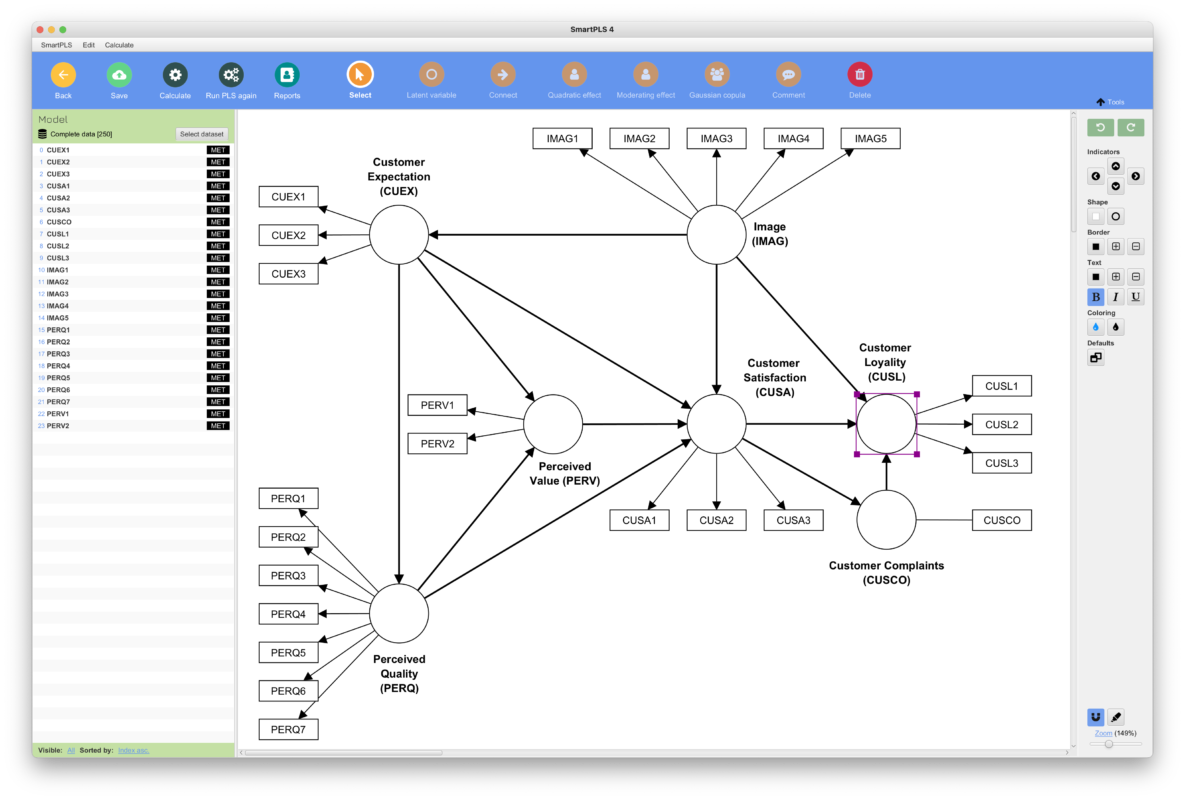
آموزش نرم افزار معادلات ساختاری SMART PLS

مقدمه

1)پیش فرض ساختارمدل ساده(حداقل در مورد رویکردهای مبتنی بر رگرسیون)،

2)پیش فرض قابل مشاهده بودن همۀ متغیرها،

3)پیش فرض اندازه گیری بدون خطای همۀ متغیرها.

این محدودیت ها قابلیت استفاده از این روش ها را در برخی از موقعیت های پژوهشی محدود می سازد.فرض ساختار مدل ساده(یک متغیر وابسته و چندین متغیر مستقل)راجاکوبی(1978)این گونه مورد نقد قرار می دهد که:ما در یک دنیای پیچیده و چند متغیره زندگی می کنیم،باید در نظر داشته باشیم مطالعۀ اثریک یا دو متغیر به صورت مجزا،نسبتاً کاذب وغیرمنطقی است.اگرچه در مدل سازی ها برخی از جنبه های واقعیت نادیده گرفته می شوند(شوگان،2002)اما این پیش فرض در رویکردهای رگرسیونی ممکن است تحلیل موقعیت های پیچیده و واقعی را بسیارمحدود کند.بویژه هنگامی که هدف تعیین اثرات بالقوه متغیرهای میانجی یاواسطه ای بر ارتباط بین متغیرهای مستقل و وابسته باشد،که ممکن است ناشی از تأثیربرخی متغیرهای وابسته بر متغیرهای وابسته دیگر باشد.در مورد محدودیت پیش فرض دوم،مک دونالد(1996)تأکید می کند که یک متغیر فقط زمانی می تواند قابل مشاهده نامیده شود که ارزش آن از طریق نمونه گیری دنیای واقعی به دست آید.بنابراین هرمتغیری که مستقیماً باهرچیز قابل مشاهده مطابقت نداشته باشد باید به عنوان غیر قابل مشاهده درنظر گرفته شود(دیجکسترا،1983).بر اساس این تعریف تنها برخی از متغیرها مانند سن و جنسیت متغیرهای قابل مشاهده تلقی می شوند،حال آن که اثر ومشخصات مولکول ها،فرایندها،ژن ها،ویروس ها وباکتری ها معمولاً به صورت غیر مستقیم مشاهده می شوند(والد،1993).درمورد این فرض که همۀ متغیرها بدون خطا اندازه گیری می شوند،باید دانست هر مشاهده ای از دنیای واقعی با خطا های اندازه گیری خاصی همراه است،که از دوبخش تشکیل می شوند(باگوزی،یی و فیلیپس،1991).نخست خطای تصادفی که از ترتیب گویه ها در پرسشنامه یا خستگی پاسخگو ناشی می شود(هیلر و رای،1972) و دوم خطای منظم،از قبیل واریانس روش(نسبت دادن واریانس به روش اندازه گیری به جای سازۀ مورد بررسی)(باگوزی و همکاران،1991).به دلیل اینکه نمره مشاهده شدۀ یک گویه از سه بخش تشکیل شده است،یعنی نمره واقعی متغیر،خطای تصادفی و خطای منظم.با دید دقیق تر می توان گفت روش های پیشین ،تنها هنگامی قابل استفاده هستند که مولفه های خطای منظم وتصادفی نداشته باشند که این امر به ندرت در واقعیت امکان پذیر است(هین لاین و کاپلان،2004).

مدل یابی معادلات ساختاری

برای غلبه برمحدودیت های روش های پیشین،نویسندگان به طور فزاینده ای از مدل یابی معادلات ساختاری به عنوان یک راه حل مناسب استفاده کردند.در مقایسه با روش های رگرسیونی،که درآنها فقط یک سطح از رابطۀ بین متغیرهای مستقل و وابسته به صورت همزمان تحلیل می شوند،درمدل یابی معادلات ساختاری به عنوان روش ثانویه امکان مدل یابی ارتباط میان چندین سازۀ مستقل و وابسته وجود دارد(گفن،اشتراب و بودرئو،2000).بنابراین در این دو روش تفاوتی بین متغیرهای مستقل و وابسته نیست،بلکه بین متغیرهای مکنون درون زا(متغیرهایی که تحت تاثیر عوامل درون مدل قرار دارند)و برون زا(متغیرهایی که تحت تاثیرعوامل خارج از مدل قرار دارند)تمایز وجود دارد.مزیتی که روش های مبتنی بر مدل یابی معادلات ساختاری نسبت به روش های پیشین دارند،انعطاف پذیری این روش ها در بررسی اثر متقابل نظریه وداده ها است.اگرمبانی نظری قوی باشد،محققان می توانند در تحلیل داده ها بیشتر به نظریه متکی شوند و هنگامی که مبانی نظری قابل اطمینانی وجود نداشته باشد محققان می توانند بیشتر به داده های تجربی متکی شوند.در مدل یابی معادلات ساختاری این امکان فراهم می شود تا متغیرهای مکنون به وسیله نشانگرها اندازه گیری شده و خطای انداره گیری در مدل،مورد بررسی قرار گیرد(چین،1998).بنابراین،محققان می توانند با استفاده از این روش ها برمحدودیت های روش های پیشین غلبه کرده واین امکان را بیابند که فرض های مورد اندازه گیری و نظری را به کمک روش تحلیل عاملی تاییدی در برابر داده های تجربی،به روش آماری آزمون کنند.به طور کلی می توان گفت، روش های مدل یابی معادلات ساختاری،تعمیم وگسترش روش های پیشین از قبیل رگرسیون وتحلیل عاملی است.براساس رویکردهای مبتنی برمدل یابی معادلات ساختاری،محققان علوم مختلف می توانند رابطۀ علّی میان چند متغیر پیش بین و وابسطه را حتی زمانی که این روابط پیچیده باشند،بررسی کنند.این امر ازطریق معادله های ساختاری سلسله مراتبی یا غیرسلسله مراتبی،بازگشتی یا غیرقابل بازگشتی قابل آزمون می باشد.علاوه بر این محققان می توانند متغیرهای مکنون وخطای مدل های اندازه گیری راتعیین کنندوباانعطاف بیشتری مدل نظری نزدیک به واقعیتی راطرح نموده و آن رادر برابر داده های واقعی به آزمون بگذارند.روش های مدل یابی معادلات ساختاری ازقبیل لیزرل وکمترین مجذورات جزئی(PLS)روش های جدید تحلیل داده ها محسوب می شوند.در مقایسه با ابزارهای آماری پیشین،از طریق مدل یابی معادلات ساختاری می توان مجموعه ای از سوالات پژوهشی مرتبط به هم را در یک تحلیل واحد،منظم و جامع مورد آزمون قرار داد.علاوه بر این می توان روابط میان چندین سازۀ مستقل و وابسته را به صورت همزمان بررسی نمود.ویژگی تحلیل همزمان در یک مدل به صورت یکپارچه این روش را ازمدل های رگرسیون خطی که تنها یک سطح از رابطه بین متغیرهای مستقل ویک وابسته در یک زمان مورد تحلیل قرار می گیرد،متمایز می سازد.به طور کلّی ،برای برآورد پارامترها در مدل یابی معادلات ساختاری می توان از روش مبتنی بر کوواریانس و روش مبتنی بر واریانس(یامبتنی بر مؤلّفه)استفاده کرد.مدل یابی معادلات ساختاری مبتنی بر کوواریانس بویژه در طول چند دهه گذشته اهمیت زیادی پیدا کرده است.این امر باعث شده بسیاری از محققان علوم اجتماعی،روش مبتنی بر کوواریانس را به اشتباه مترداف با اصطلاح مدل یابی معادلات ساختاری در نظربگیرند(چین،1998).اگر چه نرم افزارهای متفاوتی برای انجام این نوع از تحلیل استفاده شده اند که می توان به نرم افزارهایی چون COSAN،SEPATH،AMOS،EQSاشاره کرد،اما برنامه لیزرل که به وسیله جورسکاگ در سال 1975به وجود آمد بیشتر رواج یافته است،به طوری که گاهی روش لیزرل مترادف با مدل یابی معادلات ساختاری مبتنی بر کوواریانس به کار می رود.برخلاف روش های رگرسیونی،در مدل یابی معادلات ساختاری،نه تنها مدل ساختاری ارزیابی می شود(علّیت فرض شدۀ میان مجموعه ای از سازه های وابسته و مستقل)،بلکه مدل اندازه گیری(بارهای عاملی گویه های مشاهده شده بر روی متغیرهای مکنون آنها)نیز مورد بررسی قرار می گیرد. تحلیل همزمان مدل اندازه گیری و مدل ساختاری این امکان را فراهم می سازد تا خطاهای اندازه گیری متغیرهای مشاهده شده به عنوان بخشی از مدل،همراه با آزمون فرضیه ها تحلیل شوند.

مدل یابی معادلات ساختار مبتنی برکوواریانس

در مدل یابی معادلات ساختاری مبتنی بر کوواریانس با استفاده از تابع حداکثر درست نمایی تلاش می شود تا تفاوت بین کوواریانس های نمونه که بوسیله مدل نظری پیش بینی می شود کمینه گردد.بنابراین در این روش،از طریق پارامترهای برآورد شده،ماتریس کوواریانس داده های گردآوری شده باز تولید می شوند.علاوه بر این رعایت مفروضه های نرمال بودن چندمتغیره واستقلال مشاهده ها از یکدیگر،شرط اساسی مدل یابی معادلات ساختاری است. روش های مبتنی بر کوواریانس در بین روش های مدل یابی معادلات ساختاری،به مراتب شناخته شده تر هستند.با این وجود،روشی دیگر با رواج کمتر با عنوان کمترین مجذورات جزئی(PLS)،برای محققان علاقه مند در انجام تحلیل های مبتنی بر مدل یابی معادلات ساختاری می تواند مفید باشد.

مدل یابی معادلات ساختاری مبتنی بر حداقل مجذورات جزئی

پیدایش رویکرد PLS به زمانی بر می گردد که هرمان والد(1975) دو روش از سرگیری با استفاده از برآورد کمترین مجذورات برای مدل های یک مؤلفه ای و چند مؤلفه ای و همبستگی بنیادی را معرّفی کرد. انگیزه رشد PLS توسط والد یافتن وضعیتی بود که بین تحلیل داده ها و مدل یابی سنتی باشد زیرا مدل یابی سنتی دارای مفروضه سخت گیرانه در مورد توزیع احتمالی داده ها بود ولی رویکرد PLS نابسته به توزیع بود.کمترین مجذورات جزئی روش نسبتاً جدیدی از معادلات ساختاری رگرسیونی است.این روش هم برای رگرسیون تک متغیری و هم چند متغیری وبا چند متغیر وابسته کاربرد دارد.برای بررسی ارتباط بین متغیرهای وابسته و متغیرهای مستقل،PLS متغیرهای تبیینی یا مستقل جدیدی ایجاد می کند که غالباً عامل،متغیرمکنون یا مؤلّفه ها نامیده می شوند.این مؤلفه ها ترکیب خطی از نشانگرهای خود هستند.PLS بر اساس برآورد کمترین مجذورات با هدف اولّیۀ بهینه ساختن تبیین واریانس در سازه های وابسته مدل های معادلات ساختاری است.روش PLS در ابتدا برای تحلیل موقعیت ها یا مدل های بسیار پیچیده ای به کار می رود که اطلاعات نظری کمی در مورد آنها وجود دارد،یا اینکه هدف از آزمون این مدل ها پیش بینی یا کاربرد است.بر خلاف مدل یابی معادلات ساختاری مبتنی برکوواریانس که میزان برازش مدل مفروض را ارزیابی می کند و در نتیجه برآورد مدل در جهت تبیین،آزمون و تائید نظریه است،روش PLSپیش بینی مدار بوده،به نظریه قوی نیاز ندارد و به عنوان روش ساخت نظریه می تواند به کار رود(وینزی و همکاران،2010).PLSدر ابتدا برای استفاده در رشته اقتصادسنجی توسعه یافت،اما در رشتۀ شیمی نیز برای استفاده در تحقیقات شیمی تجزیه،فیزیک و پزشکی مورد استقبال قرار گرفت.همچنین در رشته های مدیریت و بازاریابی نیز کاربردهای فراوانی دارد.کمترین مجذورات جزئی((PLS در علوم پایه بویژه شیمی وغیره،یعنی در علومی که تعداد زیادی از متغیرهای همبسته و تعداد محدودی از مشاهده شده ها وجود دارند،کاربرد فراوانی دارد.هدف والد(1975)توجه به نظریه ها وداده های ضعیف بود.به همین دلیل PLSرا به وجود آورد.کمترین مجذورات جزئی برای مقابله با مشکلات داده های خاص مانند حجم اندک داده ها،وجود داده های گم شده و هم خطی بین متغیرهای مستقل طراحی شده است.در مقابل،کمترین مجذورات متداول(OLS)نسبت به حجم اندک داده ها،داده های گم شده و هم خطی چندگانه مقاوم نبوده ونتایج بی ثباتی را ایجاد می کند،زیرا این شرایط باعث تورم خطای استاندارد ضرایب برآورد شده می گردد.هدف کمترین مجذورات جزئی،پیش بینیYازX و توصیف سازه های زیربنایی مشترک دو متغیراست.کمترین مجذورات جزئی روش رگرسیون برای شناسایی عامل های زیر بنایی است که از ترکیب خطی متغیرهای تبیینی یا X،بهترین مدل پاسخ یا پیش بین متغیرهایYرا فراهم می سازد.در واقع مدل PLSبه دنبال کشف بهترین پیش بین متغیرهای وابسته از روی متغیرهای مستقل است.کمترین مجذورات جزئی گاهی اوقات “مدل یابی نرم” نامیده می شود.زیرا در صورتی که OLS فرض های سخت گیرانه ای مانند عدم وجود هم خطی چند گانه بین متغیرهای مستقل دارد،مدل یابی نرم اشاره به برخورد انعطاف پذیرانه با این فرض های اساسی دارد.کمترین مجذورات جزئی به عنوان یک روش خطی،پیش بینی و تبیینی ونه تفسیری معّرفی می شود.استفاده از این روش،قبل از استفاده روش های تفسیری مانند رگرسیون خطی چندگانه یا SEM توصیه می گردد.کمترین مجذورات جزئی،رابطۀ خطی بهینه بین متغیرهای مکنون را نشان می دهد و می توان از آن به عنوان بهترین ترکیب متغیرهای پیش بین در یک بررسی با وجود همۀ محدودیت های مفروض تعبیرکرد.کمترین مجذورات جزئی به عنوان روش گسترش یافته رگرسیون خطی چندگانه فرض های مشابه زیادی با آن دارد؛مثلاً خطی بودن ونداشتن داده های دورافتاده در هنگام استفاده از کمترین مجذورات جزئی است.باید توجه کرد که به دلیل آنکه توزیع کمترین مجذورات ناشناخته است،آزمون معنا داری متداولی وجود ندارد.در هرصورت معنا داری مسیر ها ازطریق روش های خود گردان سازی یا بوت استراپ و یا برش متقاطع یا جک نایف که روش های باز نمونه گیری هستند،آزمون می شوند.این روش،مشابهت هایی با روش رگرسیون مؤلّفه های اصلی (PCR) دارد که در آن مؤلّفه های اصلی به عنوان متغیرهای وابسته در رگرسیون است.تفاوت عمده PLS با PCR این است که مؤلّفه های اصلی تنها با مقادیر متغیرهایX تعیین می شود،در صورتی که با PLS،مقادیر هر دو متغیرهای X و Y در ساخت مؤلّفه ها تأثیرمی گذارند.هدف PLS تشکیل مؤلّفه هایی است که بیشترین اطلاعات لازم برای پیش بینی از متغیرهای X را به دست دهد،در صورتی که رگرسیون مؤلّفه اصلی کاهش ابعاد متغیرهای X در قالب متغیرهای معدود است.PLS بویژه زمانی برای تشکیل معادلات پیش بینی مفید است که متغیرهای تبیینی زیاد، وداده های نمونه نسبتاً کم باشد(کلاین،2011).بر خلاف مدل یابی معادلات ساختاری مبتنی بر کوواریانس،کمترین مجذورات جزئی(PLS) به جای باز تولید ماتریس کوواریانس تجربی،بر بیشترین واریانس تعیین شدۀ متغیرهای وابسته به وسیله متغیرهای مستقل تمرکز دارد.همانند هر مدل یابی معادلات ساختاری، مدل کمترین مجذورات جزئی از یک بخش ساختاری که ارتباط بین متغیرهای مکنون را نشان می دهد و یک قسمت اندازه گیری که نحوه ارتباط متغیرهای مکنون و نشانگرهای آنها را منعکس می کند،تشکیل شده است.افزون بر این،کمترین مجذورات جزئی دارای یک بخش سومی به نام”نسبت وزنی”است که برای برآورد مقادیر موردها یا نمره های عاملی افراد نمونه درمتغیرهای مکنون به کار می رود(چین و نیوستد،1999).

فصل اوّل:معرّفی مفاهیم و اصطلاحات اساسی در مدل یابی معادلات ساختاری

مقدمه

مدل یابی معادلات ساختاری روش نیرومندی در تحلیل داده های چند متغیری می باشد.استفاده از این روش در سال های اخیر توجه پژوهشگران ایرانی را به خود جلب نموده و امروزه بیشتر مقالات با این روش تحلیل و انتشار می یابند.در فصل حاضر به معرّفی کلّی مدل یابی معادلات ساختاری می پردازیم.ابتدا متغیرهای مکنون وآشکار رامورد بحث قرار داده،سپس متغیرهای مکنون برون زا و درون زا را بررسی می کنیم.پس از آن مدل تحلیل عاملی،مدل متغیرمکنون کامل،نظام نمادگذاری،طراحی مسیر و مدل اندازه گیری و ساختاری را مورد بحث قرار می دهیم.در پایان بحث چند هم خطی را که یکی از مسائل مهم در کاربرد معادلات ساختاری است،شرح می دهیم.

متغیرهای مکنون در مقابل متغیرهای آشکار

در علوم رفتاری،محققان همواره علاقه مند به مطالعۀ سازه های نظری هستند که مستقیماً قابل مشاهده نیستند.این امر به متغیرها یا عامل های مکنون مصطلح شده است.خود پنداره و انگیزش در روانشناسی؛عدم اقتدار و بی هنجاری در جامعه شناسی؛توانایی کلامی و انتظار معلم در تعلیم وتربیت؛وسرمایه داری و طبقۀ اجتماعی در اقتصاد نمونه هایی از متغیرهای مکنون هستند.چون متغیرهای مکنون مستقیماً قابل مشاهده نیستند،به صورت مستقیم اندازه گیری نمی شوند.بنابراین محققان آنها را به صورت عملیاتی،بر حسب رفتارهایی که معرّف آنها هستند تعریف می کنند.به طوری که متغیرهای مکنون با متغیرهای آشکار که قابل اندازه گیری هستند،مرتبط می شوند.سپس سنجش رفتار از طریق اندازه گیری مستقیم متغیرهای مشاهده شده صورت می گیرد که به صورت غیرمستقیم متغیرهای مکنون یا سازۀ زیربنایی را می سنجند.بایدبه این نکته توجه داشت که اصطلاح رفتار در طیف وسیعی از نمره های ابزارهای اندازه گیری استفاده می شود.مثلاً مشاهده ها ممکن است پاسخ های خود گزارش دهی به مقیاس نگرش،نمره های آزمون پیشرفت ومشابه آن باشد.این نمره های اندازه گیری شده،متغیرهای آشکار یا مشاهده شده نام دارند.متغیرهای آشکار در روش شناسی مدل یابی معادلات ساختاری،به عنوان نشانگرهایی که معرّف سازه های زیربنایی فرض شده اند،شناخته می شوند.

متغیرهای مکنون برون زا در مقابل متغیرهای مکنون درون زا

تشخیص تفاوت بین متغیرهای مکنون برون زا ودرون زا در مدل یابی معادلات ساختاری مفید خواهد بود.متغیرهای مکنون برون زا همان متغیرهای مستقل هستند؛آنها علّت تغییرات در مقادیر دیگر متغیرهای مکنون در مدل هستند.تغییرات در مقادیر متغیرهای برون زا از طریق مدل تبیین نمی شود.بلکه،تحت تأثیر عامل های خارج ازمدل قرار دارند.متغیرهایی از قبیل جنسیت، سن و وضعیت اجتماعی- اقتصادی مثال هایی از این عامل های خارجی هستند.متغیرهای مکنون درون زا همان متغیرهای وابسته هستند که به صورت مستقیم یا غیرمستقیم تحت تأثیر متغیرهای برون زای موجود در مدل قرار دارند.فرض می شود که تغییر در متغیرهای برون زا از طریق مدل تبیین می شود زیرا تمام متغیرهای مکنون که بر آنها تأثیر می گذارند در مدل وجود دارند.

مدل تحلیل عاملی

قدیمی ترین و شناخته شده ترین روش آماری برای بررسی روابط بین متغیرای مکنون ومشاهده شده تحلیل عاملی است.در این رویکرد تحلیل داده ها،محققان کوواریانس میان یک مجموعه از متغیرهای مشاهده شده رابه منظور گردآوری اطلاعات درباره سازه های زیربنایی یا عامل های آنها بررسی می کنند.دو نوع تحلیل عاملی وجود دارد:تحلیل عاملی اکتشافی(EFA) وتحلیل عاملی تأییدی(CFA) که در ادامه به توضیح آنها می پردازیم.تحلیل عاملی اکتشافی برای موقعیت هایی که ارتباط بین متغیرهای مکنون وآشکار ناشناخته ونامعلوم است،طراحی شده است.بنابراین هدف تحلیل اکتشافی این است که تعیین کند چگونه و تا چه اندازه متغیرهای آشکاربا عامل های زیربنایی شان مرتبط هستند.معمولاً محققان تمایل دارند تاحداقل تعداد عامل ها که کوواریانس میان متغیرهای مشاهده شده را محاسبه می کنند شناسایی می کنند.مثلاً فرض کنید پژوهشگری ابزار جدیدی برای اندازه گیری پنج بعد خود پنداره جسمانی(سلامت،شایستگی ورزشی،ظاهرجسمانی،هماهنگی و قدرت بدنی)طراحی کرده است.پژوهشگر باید با انجام تحلیل عاملی اکتشافی تعیین کند که گویه های اندازه گیری یا متغیرهای آشکار،تا چه اندازه با پنج سازۀ مکنون مرتبط هستند.در تحلیل عاملی،این روابط از طریق بارهای عاملی مشخص می شوند.پژوهشگرباید امیدوار باشد که مثلاً گویه های طراحی شده برای سلامت،بارهای بالایی برای آن عامل و بارهای پایین یا جزئی برای چهار عامل دیگر داشته باشند.این رویکرد تحلیل عاملی،تحلیل اکتشافی نام دارد و زمانی استفاده می شود که پژوهشگر دانش قبلی در مورد اینکه گویه های یک مقیاس عامل های مورد نظر را می سنجند،ندارد.بر خلاف تحلیل عاملی اکتشافی،تحلیل عاملی تأییدی زمانی استفاده می شود که پژوهشگر دانش زیادی از سازۀ مکنون زیربنایی دارد.پژوهشگر بر اساس دانش نظری،تحقیق تجربی ومطالعات قبلی،فرض می کند بین متغیرهای مشاهده شده و عامل های بنیادی رابطه وجود دارد وسپس به آزمون این فرض می پردازد.مثلاً براساس همان مثال قبلی(خودپنداره جسمانی)،پژوهشگر باید بار های گویه های شایستگی ورزشی را فقط برای آن عامل مورد بررسی قرار دهد،نه برای عامل های دیگر مانند:سلامت، ظاهرجسمانی،هماهنگی،وقدرت بدنی.تمایزتحلیل عاملی اکتشافی از تحلیل عاملی تأییدی دارای اهمیت ویژه ای است.درتحلیل عاملی اکتشافی،داده های تجربی با هدف کشف وآشکار سازی ویژگی های خاص و روابط مورد علاقه آنها بدون آن که مدل معیّنی برداده ها تحمیل شود تجسس می شوند.اما درتحلیل عاملی تأییدی،پژوهشگر به دنبال تهیۀ مدلی است که فرض می شود داده های تجربی را بر پایه چند پارامتر نسبتاً اندک،توصیف یا تبیین می کند.این مدل نیز مبتنی بر اطلاعات پیش تجربی درباره ی ساختار داده هاست.مدل مورد مورد نظر می تواند بر اساس:1)یک تئوری یا فریضه،2)یک طرح طبقه بندی معیّن برای گویه ها یا پاره تست ها،3)شرایط معلوم تجربی، و یا 4)دانش حاصل از مطالعات قبلی درباره ی داده های وسیع باشد.وجه تمایز بین روش های تحلیل اکتشافی و تأییدی در این است که روش اکتشافی وتأییدی در این است که روش اکتشافی با صرفه ترین روش تبیین واریانس مشترک زیربنایی یک ماتریس همبستگی را مشخص می کند.در حالی که روش های تأییدی تعیین می کنند که داده ها با یک ساختارعاملی معیّن هماهنگ هستند یا نه.تحلیل تأییدی در واقع یک روش آزمون تئوری است که درآن پژوهشگر تحلیل خود را با یک فرضیه قبلی آغاز می کند.این مدل که مبتنی بر یک شالوده نظری و تجربی قوی است، مشخص می کند که کدام متغیرها با کدام عامل ها و کدام عامل با کدام عامل ها باید همبسته شوند. علاوه برآن این روش برای ارزیابی روایی سازه نیز یک روش قابل اعتماد به پژوهشگر عرضه می کند، تا از این طریق بتواند فرضیه هایی را درباره ساختارعاملی داده ها که ناشی از یک مدل نظری از پیش تعیین شده با تعداد و ترکیب مشخصی از عامل هاست،بیازماید.

مدل متغیر مکنون کامل

در مقابل مدل های تحلیل عاملی، مدل متغیر مکنون کامل، بررسی ساختار رگرسیون میان متغیرهای مکنون را ممکن می سازد.پژوهشگر در مدل یابی علّی فرض می کند که یک سازۀ مکنون بر دیگری اثر دارد این مدل،مدل کامل نام دارد چون هر دو مدل اندازه گیری و ساختاری را در بر می گیرد.مدل اندازه گیری رابطۀ بین متغیرهای مکنون و متغیرهای اندازه گیری شده یا نشانگرهای آنها را نشان می دهد(یعنی مدلCFA) و مدل ساختاری رابطۀ میان متغیرهای مکنون را نشان می دهد.یک مدل متغیر مکنون کامل که جهت علّی را تنها از یک جهت مشخص می کند مدل غیربازگشتی نام دارد اما مدلی که رابطۀ دو جانبه را ممکن می سازد مدل بازگشتی نام دارد.

نظام نماد گذاری

مدل یابی معادلات ساختاری با استفاده از چهار نماد هندسی شکل بندی می شود:دایره(یا بیضی)، مربع(یا مستطیل)،پیکان یک طرفه وپیکان دو طرفه. به صورت قراردادی، دایره(یا بیضی) معرّف متغیرهای مکنون غیر قابل مشاهده، مربع(یا مستطیل) معرّف متغیرهای قابل مشاهده، پیکان یک طرفه معرّف اثر یک متغیر بر دیگری و پیکان دو طرفه معرّف کوواریانس یا همبستگی بین دو متغیر است. در ساخت یک الگو یا مدل بررسی، پژوهشگر از این نمادها که هر کدام در فرآیند تحلیل معرّف یک مؤلّفه مهم هستند استفاده می کند.هر یک از نمادها به صورت مختصر در ذیل توصیف می شوند:***********

نمودار مسیر

ارائه طرحی از مدل ها نمودار مسیر نامیده می شود. زیرا تصویری از روابطی که میان متغیرهای مورد مطالعه وجود دارد را ترسیم می کند.در اصل، همان طور که خواهید دید،نمودار مسیر مدل معادلات ساختاری، مجموعه ای از روابط بین متغیرهای وابسته و متغیرهای مستقل را نشان می دهد. همچنین نشان داده خواهد شد که چگونه چهار نماد ذکر شدۀ فوق، فرآیند علّی خاصی را نشان می دهند. با استفاده از شکل1-1 در این رابطه بحث می کنیم.در مدل شکل1-1 دو متغیر مکنون وجود دارد،خودپنداره ریاضی(MSC) و پیشرفت ریاضی(MATH) و پنج متغیر آشکار-سه متغیر برای اندازه گیری خودپنداره ریاضی(SDQMSC; APIMSC; SPPCMSC) ودو متغیر آشکار(MATHGR; MATHACH) برای اندازه گیری پیشرفت ریاضی در نظر گرفته شده اند.این پنج متغیر آشکار به عنوان نشانگرهای عوامل مکنون عمل می کنند.

شکل 1-1 مدل نظری معادلات ساختاری

در ارتباط با هر کدام از متغیرهای مشاهده شده یک ضریب خطا(err1-err5) و برای متغیر مکنون پیش بینی شده یک ضریب پس ماند (Resid1) وجود دارد.تمایز مهمی بین ضریب خطا و ضریب پس ماند وجود دارد.ضریب خطا با متغیرهای مشاهده شده مرتبط است و خطای اندازه گیری را نشان می دهد که معرّف کفایت در اندازه گیری عامل بنیادی مرتبط با آن است.خطای اندازه گیری از دو منبع ناشی می شود: خطای اندازه گیری تصادفی و منحصر به فرد بودن خطا.منحصر به فرد بودن خطا برای توصیف واریانس خطای به وجود آمده از بعضی ویژگی های خاص به کار می رود.چنین خطایی اغلب خطای تصادفی منظم نامیده می شود.خطای پس ماند معرّف خطا در پیش بینی عامل های درون زا از طریق عامل های برون زا است.مثلاً ضریب پس ماند نشان داده شده در شکل1-1 نشانگر خطا در پیش بینی پیشرفت ریاضی به وسیله خودپنداره ریاضی است.

معادله های ساختاری

مدل یابی معادلات ساختاری از طریق مجموعه ای از معادلات رگرسیون یا ساختاری نشان داده می شود. زیرا 1)معادله های رگرسیون،اثر یک یا چند متغیر را بر یکدیگر نشان می دهند،2)این تأثیر،در مدل یابی معادلات ساختاری، از طریق پیکان های یک طرفه از متغیر عامل یا مستقل به متغیر وابسته نشان داده می شود.به منظور نشان دادن این تفسیر از معادلات رگرسیون در مدل یابی معادلات ساختاری،به شکل1-1 توجه کنید.می بینیم که شش متغیر با پیکان هایی که به طرف آنها ترسیم شده است وجود دارد،پنج تا از آنان نشان دهندۀ متغیرهای قابل مشاهده (SDQMSC, APIMSC, SPPCMSC, MATHGR,MATHACH) هستند و یکی نشان دهندۀ متغیر مکنون (یا عامل،MATH) می باشد. بنابراین،توابع رگرسیون در شکل1-1 برحسب شش معادله مجزا به صورت زیر خلاصه می شوند:

MATH=MSC+resid1

SDQMSC=MSC+err1

APIMSC=MSC+err2

SPPCMSC=MSC+err3

MATHGR=MATH+err4

MATHACH=MATH+err5

ساخت یا ترکیب اساسی مدل یابی معادلات ساختاری

مدل معادلات ساختاری از دو مدل فرعی یعنی مدل اندازه گیری و مدل ساختاری تشکیل شده است. مدل اندازه گیری،رابطۀ بین متغیرهای آشکار ومکنون را نشان می دهد.به عبارت دیگر،رابطۀ بین نمرات ابزار اندازه گیری(متغیرهای نشانگر یا مشاهده شده) و سازۀ زیربنایی(یعنی متغیر مکنون) که هدف، سنجش آن از طریق نشانگرهاست را مشخص می کند. مدل اندازه گیری همان مدل تحلیل عاملی تأییدی است که در ابتدای این فصل توضیح داده شده. در مقابل، مدل ساختاری، رابطۀ میان متغیرهای مکنون را نشان می دهد. مدل ساختاری اثرات مستقیم و غیرمستقیمی که متغیر مکنون خاصی بر متغیرهای مکنون دیگر موجود در مدل دارد را نشان می دهد. همان طور که در شکل2-1 مشاهده می کنید، مؤلّفه های اندازه گیری وساختاری مشخص شده اند. عناصر مدل داخل هر مستطیل نشان دهندۀ یک مدل تحلیل عاملی تأییدی هستند ودو عامل مکنون در درون بیضی،معرّف مدل ساختاری است.مدل تحلیل عاملی تأییدی در سمت چپ نمودار مدل یک عاملی خودپنداره ریاضی(MSC) را نشان می دهد که از طریق سه متغیر مشاهده شده(SDQMSC, APIMSC, SPPCMSC) اندازه گیری می شود ومدل تحلیل عاملی تأییدی در سمت راست مدل تک عاملی پیشرفت ریاضی(MATH) را نشان می دهد که از طریق دو متغیر مشاهده شده(MATHGR-MATHACH) اندازه گیری می شود.در هر دو مدل،ضریب رگرسیون متغیرهای مشاهده شده برای هر عامل،واریانس عامل وخطای اندازه گیری مشخص شده است.

شکل2-1 مدل ساختاری به همراه دو مدل اندازه گیری و مدل ساختاری

در ادامه به معرّفی علائمی که در مدل معادلات ساختاری و مدل اندازه گیری استفاده می شود،می پردازیم.در مدل ساختاری از علائم زیر استفاده می شود:

****برای متغیرهای مکنون برون زا به کار برده می شود و Xi یا Ksi نام دارد.

****:متغیر مکنون درون زا است که اتا(Eta) نامیده می شود.

****:رابط مسیرهای***به***که ضریب گاما نامیده می شود.

****:رابط مسیرهای یک ***به***دیگری که بتا(Beta) نامیده می شود.

****:ماتریس همبستگی مشترک میان***ها که فای(Phi) نامیده می شود.

****:ماتریس همبستگی مشترک میان ضرایب خطای***که سای Psi نامیده می شود.

****: ضرایب خطا که به عنوان زتا(***) شناخته شده اند.

مدل اندازه گیری:

متغیرهای*** وY، که مشاهده ها یا داده های واقعی جمع آوری شده هستند.X و Y به ترتیب سازه های برون زا و درون زا را اندازه گیری می کنند.

لامبدا(X***( X:مسیر بین متغیر های مشاهده شدۀ Xو*** را نشان می دهد.

تتا دلتا(******) که واریانس خطای مرتبط با آیتم های X را نشان می دهد.واریانسی که متغیرهایی مکنون برون زا را منعکس نمی کند.

لامبداY (Y***):مسیر بین متغیرهای مشاهده شدۀY و متغیرهای مکنون درون زا را نشان می دهد.

تتا اپسیلون(*****) که معرّف واریانس خطای مرتبط با آیتم هایY است.یعنی واریانسی که متغیرهای مکنون درون زا را منعکس نمی کند. شکل3-1 علائم ذکر شده در فوق را نشان می دهد.

مدل: معرّف رابطۀ ساختار فرض شدۀ متغیرهای قابل مشاهده با متغیرهای پنهان و همچنین رابطۀ متغیرهای پنهان با یکدیگر است.

پس ماند: تفاوت بین مدل فرض شده و داده های مشاهده شده را نشان می دهد.اصطلاح پس ماند خطا نیز نامیده می شود.

علّت: اثر مستقیم یک متغیر بر دیگری در چارچوب مدل است.اندازه و جهت آن از طریق ضرایب رگرسیون مشخص می شود.

شکل3-1 مدل معادلات ساختاری به همراه علائم

هم خطی چندگانه

یکی از مسائلی که پژوهشگران هنگام استفاده از طرح های همبستگی(از قبیل رگرسیون و مدل یابی معادلات ساختاری) با آن مواجه می شوند،هم خطی چندگانه است. این مشکل زمانی بروز می کند که همبستگی بعضی از متغیرها با هم بسیار زیاد باشد(مثلاً بیشتر از 85/0). این امر انجام برخی از اعمال خاص ریاضی را روی داده ها ناممکن یا ناپایدار می سازد؛ زیرا در برخی موارد، مخرج کسرها نزدیک به صفر می شوند.اغلب، هم خطی چندگانه زمانی بروز می کند که متغیرهای متفاوت در واقع چیز واحدی را اندازه گیری می کنند.فرض کنید که X مقیاسی برای اندازه گیری فقر، و Y مقیاسی برای بیکاری است. اگر 9/0=r_xy باشد در این صورت متغیرهای X و Y زائد هستند.در این حالت به جای هر دو متغیر می توان از یک متغیر برای تحلیل استفاده کرد.زیرا مقیاس فقر متمایز از مقیاس بیکاری نیست و فقط یکی از متغیرها باید وارد تحلیل شود.هم خطی چندگانه می تواند بین متغیرهای مکنون، وقتی که همبستگی برآورد شدۀ آنها بسیار بالا باشد هم اتفاق بیافتد. این امر نشانگر آن است که آنها متغیرهای متمایزی از یکدیگر نیستند. علاوه بر موارد فوق، پژوهشگران نیز زمانی که متغیرهای ترکیبی و متغیرهای سازنده آنها باهمدیگر تحلیل می شوند، ممکن است سهوا باعث هم خطی چندگانه شوند. فرض کنید پرسشنامه ای از10 گویه تشکیل شده است و مجموع این ده گویه نیز محاسبه شده است. در این صورت اگرچه ممکن است همبستگی دو متغیری بین نمره کل و هر یک از گویه ها خیلی زیاد نباشد، اما همبستگی چندگانه بین نمره کل و این ده گویه برابر با یک است که در این حالت هم خطی چندگانه در بیشترین حد خود قرار دارد. تشخیص هم خطی چندگانه بین یک جفت از متغیرها بسیار ساده است و می توان با استفاده از ماتریس همبستگی به این امر پی برد. اما تشخیص این امر ^{برای بیش از دو متغیر به سادگی امکان پذیر نیست. به مثال10 گویه توجه کنید که هیچ یک از همبستگی های دو} متغیری گویه ها با نمره کل بالا نیست. در این صورت برای تشخیص هم خطی چندگانه، یک روش محاسبه مجذور همبستگی چندگانه بین هر متغیر با کل مجموعه است. 9/0<R²smc نشانگر هم خطی چندگانه است. آماره دیگر تلرانس یا ضریب تحمل می باشد که برابر با1-R²smc می باشد و نشان دهندۀ میزان واریانسی است که همۀ متغیرها نتوانسته اند تبیین کنند.تلرانس کمتر از 1/0 نشانگر هم خطی چندگانه است. آماره دیگر عامل تورم واریانس (VIF) می باشد. این آماره مساوی با(1-R²smc)/1 است که نسبت واریانس استاندارد شده بر واریانس خطا می باشد. VIF>10 نشانگر زائد بودن متغیرهاست.دو راه اساسی برای مواجهه با هم خطی چندگانه وجود دارد:حذف متغیرها یا ترکیب متغیرهای زائد و ساخت یک متغیر ترکیبی. برای مثال اگرX و Y همبستگی بالایی با یکدیگر داشته باشند، می توان یکی از آنها را حذف کرد یا می توان با جمع بستن نمرات آنها یک متغیر جدید تعریف کرد. ولی باید توجه داشت که نمره کل باید جایگزین X وY در تحلیل شود.

فصل دوم:روش شناسی کمترین مجذورات جزئی(PLS)

مقدمه

مدل مسیر کمترین مجذورات جزئی با دو مجموعه از معادلات خطی تعریف شده است: مدل درونی و مدل بیرونی.یا مدل ساختاری، رابطۀ بین متغیرهای مکنون و مدل بیرونی یا مدل اندازه گیری، ارتباط بین متغیرهای مکنون و نشانگرهای مشاهده شده را معیّن می کند.در ادبیات پژوهشی اصطلاحات یکسانی برای این دو مفهوم به کار نمی رود. برای نمونه،در مدل یابی معادلات ساختاری مبتنی بر کوواریانس، مفاهیم مدل های ساختاری و مدل های اندازه گیری را به کار می برند؛ ولی در مدل مسیر PLS از اصطلاحات مدل درونی و مدل بیرونی استفاده می شود. در شکل1-2 مثالی از مدل درونی و بیرونی برای مدل مسیر PLS نشان داده شده است.

شکل1-2: مدل مسیر PLS

شهرت مدل یابی مسیر PLS در میان دانشمندان و کاربران، ریشه در چهار ویژگی دارد: اوّل اینکه به جای ترسیم مدل اندازه گیری به صورت انعکاسی رایج،الگوریتم مدل یابی مسیر PLS امکان محاسبه انواع متعددی از روابط علّت و معلولی مدل هایی را فراهم می آورد که از هر دو نوع مدل اندازه گیری(انعکاسی و تشکیل دهنده یا تشکیلی) به وجود آمده اند. دوم اینکه PLS در برآورد مدل های مسیر با حجم نمونۀ کوچک کارآیی دارد. سوم اینکه در این روش ضرایب مسیر مدل های PLS خیلی پیچیده(مدل های تشکیل شده از متغیرهای مکنون و آشکار زیاد) بدون مشکل برآورد می شوند. مزایای روش شناختی مدل یابی مسیر PLS نسبت به CBSEM یا مدل یابی مبتنی بر کوواریانس زمانی بارز می شود که با احتمال وقوع عدم همگرایی یا نتایج نامناسب روبرو شویم به عنوان مثال، هنگامی که تعداد متغیرهای مکنون و آشکار نسبت به تعداد مشاهده ها بالا بوده و یا تعداد نشانگرهای هر متغیر مکنون پایین است، در این وضعیت ها PLS نسبت به CBSEM مناسب بوده و به نتایج همگرا منجر می شود که محققان زیادی به این نکته تاکید دارند. مثلاً حنفی (2007) اظهار می کند که همگرایی (PLS) همیشه در عمل تأیید شده است. ویژگی چهارم اینکه مدل یابی مسیر PLS هنگامی کاربرد دارد که توزیع ها چولگی بالایی دارند. زیرا ویژگی های توزیع از قبیل نرمال بودن از فرض های این روش نیست. با توجه به این ویژگی، هرمن والد آن را به عنوان مدل نرم معرّفی کرد که با مدل یابی معادلات ساختاری که بر فرض های نسبتاً سختی تکیه می کند متفاوت است. علاوه برآن وجود نرم افزارهای مدرن و آسان PLS مانند SmartPLS و Visua1PLS سبب جذابیت بیشتر PLS شده است. در این فصل به معرّفی و بررسی ویژگی های روش شناختی PLS می پردازیم. این فصل شامل معرّفی مدل های اندازه گیری انعکاسی و تشکیل دهنده یا تشکیلی، الگوریتم PLS و حجم نمونه و مقاوم بودن برآورد پارامترها می باشد.

مدل های اندازه گیری تشکیل دهنده (مدل B) و انعکاسی (مدل A)

مدل های معادلات ساختاری معمولاًمتغیرهای مکنون را با نشانگرهای چندگانه نشان می دهند.مدل اندازه گیری یا مدل بیرونی رابطۀ بین نشانگرها ومتغیرهای مکنون را مشخص می کند. جهت رابطه های مسیر در هر مدل اندازه گیری با توجه به جهت بین متغیر مکنون و نشانگرهای شان از طریق روش تشکیل دهنده و انعکاسی توصیف می شود. مدل اندازه گیری انعکاسی یا مدل A ریشه در نظریه آزمون کلاسیک و روان سنجی دارد.در این مدل هر نشانگر معرّف یک اندازه گیری توام با خطا از متغیر مکنون است. همچنین در این مدل جهت علّیت از سازه به نشانگرهاست ؛ یعنی فرض می شود اندازه گیری های مشاهده شده، تغییر در متغیر مکنون را منعکس می کنند.به عبارت دیگر با تغیر در سازۀ مورد نظر،تغییرات در همۀ نشانگرها بارز می شود(هیر و همکاران،2006)شکل2-2 نمونه ای از مدل اندازه گیری انعکاسی را نشان می دهد.

شکل2-2 مدل اندازه گیری انعکاسی

عزّت نفس مثالی از مدل اندازه گیری بر اساس نشانگرهای انعکاسی می باشد همان طور که در شکل3-2 می بینیم دو نشانگر باور خود توانمندی به معنای داشتن اطمینان به توانایی فکر کردن،درک کردن، آموختن،انتخاب کردن و تصمیم گیری برای خود و دیگری احترام به خود یا داشتن حرمت نفس به معنای ارزش برای خود یعنی آن که به خود حق بدهیم که زندگی کنیم و شاد باشیم،به عنوان نشانگرهای انعکاسی عزت نفس در نظرگرفته شده اند.

شکل3-2 مدل اندازه گیری انعکاسی (عزت نفس)

نشانگرهای انعکاسی وابسته به متغیر مکنون هستند.
این نشانگرها باید همبستگی مثبت بالایی با یکدیگر داشته باشند.
مثال:عزت نفس

_ باور به خودتوانمندی

_ حرمت نفس یا احترام به خود

نشانگرهای انعکاسی بر اساس دیدگاهی که همۀ آنها پدیده زیربنایی یکسانی(متغیرهای مکنون) را اندازه گیری می کنند به وجود آمده اند.در این نوع مدل اندازه گیری با تغییر در سطح واقعی پدیده(مثلاً کاهش در مقدار)، همۀ نشانگرها باید در جهت مشابهی تغییر یابند.مقدار تغییری که هر کدام از نشانگرها نسبت به تغییر در پدیده زیربنایی دارند، اساسی برای ارتباط با متغیرهای مکنون است.کیفیت انعکاس نشانگرها به وسیله بارها تعیین می شود،یعنی میزان واریانسی که نشانگرها برای متغیرهای مکنون محاسبه می کنند. برای اینکه نشانگرها به صورت انعکاسی مدل یابی شوند توجه به چند نکته ضروری است. نکته اوّل نظریه حقیقی در پس مدل اندازه گیری موجود باشد. سؤال این است که پژوهشگران چگونه متغیرهای مکنون را نسبت به نشانگرها مفهوم سازی می کنند؟ اگر متغیر مکنون به عنوان علّت اندازه گیری های مشاهده شده در نظر گرفته شود، طرح مسیرها برای مدل باید به صورت انعکاسی مشخص شود. برای مثال،نگرش را در نظر بگیرید اگر پاسخ به نشانگرها تحت تأثیر آن نوع نگرش در نظر گرفته شوند، نمونه ای از این روش تلقی می شود. علاوه بر فهم نظری، نکته ای دیگر هدف مطالعه است. اگر هدف تبیین اندازه گیری های مشاهده شده باشد، باید از مدل اندازه گیری انعکاسی استفاده شود. زیرا اثر واریانس های پس ماند برای معادلات مدل اندازه گیری را کاهش می دهد. نکته آخر مربوط به پیشامد تجربی است. این امر اشاره به ثبات برآوردها، تحت تأثیر حجم نمونه و هم خطی بین متغیرهای مستقل در میان نشانگرها در هر بلوک دارد. در این رابطه مدل یابی نشانگرهای انعکاسی باید این پیچیدگی را کمینه کند زیرا پارامترهای برآورد های شده بر اساس رگرسیون ساده خواهند بود؛ یعنی اینکه مدل یابی انعکاسی در مدل هایی با پیچیدگی کمتر یا متوسط قابل کاربرد است.برای متغیرهای مکنون با نشانگرهای انعکاسی، بارها باید برای تعیین تناسب نشانگرها بررسی شوند. به ضرورت هر بار باید همبستگی بین نشانگرها و نمره مؤلّفه را نشان دهد. نشانگرهای با بارهای پایین بر این امر دلالت دارند که آنها رابطۀ پایینی بر حسب واریانس مشترک با نمره مؤلّفه متغیر مکنون دارند. در برخی از موقعیت ها، مثلاً در مراحل اوّلیه شکل دهی یک مدل، ممکن است تعیین جهت علّیّت از اندازه ها به سازه ها مناسب تر باشد. این نوع از موقعیت ها، معرّف مدل اندازه گیری، با روش تشکیل دهنده یا تشکیلی است. در این حالت یک سازه به عنوان ترکیبی از نشانگرها تعریف می شود. یک نمونه از این مدل را می توان وضعیت اجتماعی- اقتصادی در نظر گرفت که ترکیبی از متغیرها است(هیر و همکاران،2006). لازم به ذکر است که در این وضعیت متغیر مکنون به عنوان ترکیبی از نشانگرها به اضافه جمله اخلال مدل یابی می شود. روش B به مدل هایی که تنها شامل نشانگرهای تشکیل دهنده می شود اشاره دارد. در مقابل نشانگرهای انعکاسی، در نشانگرهای تشکیل دهنده این ویژگی که نشانگرها باهم مرتبط هستند و پدیده زیربنایی یکسانی را اندازه گیری می کنند وجود ندارد. در عوض نشانگرهای تشکیل دهنده به عنوان متغیرهای علّی در نظر گرفته شده اند که بر شکل گیری متغیر مکنون تأثیر دارند. یک مثال مناسب توسط کوهن،کوهن،ترزی،مارچی و ولز(1990) ارائه شده است. آنها اظهار می دارند، اندازه های مشاهده شده، تعداد کودکان در خانواده، بیماری مادر و ساعت های اشتغال مادر مثالی از نشانگرهای سازۀ مکنون دسترسی پذیری مادران برای تعامل و نظارت بر هر کودک هستند. در این وضعیت دسترسی پذیری مادران متغیر مکنون را نشان می دهد که از این نشانگرها ظاهر می شود همچنین مشخص است که تعداد کودکان در خانواده لزومأ مرتبط با سلامتی مادران نیست؛ زیرا متغیر مکنون به عنوان اثر نسبتاً علّی از پاسخ های تک تک نشانگرها شکل گرفته که ممکن است این نشانگرها ارتباطی با یکدیگر نداشته باشند و حضور یک یا هر سه این نشانگرها برای تشکیل سازۀ مکنون دسترسی پذیری کافی باشد(بولن و لنوکس،1991).کوهن وهمکاران نشان دادند تعداد قابل توجهی از تحقیقات منتشر شده به روش مدل یابی معادلات ساختاری مبتنی بر کوواریانس، در حقیقت از نشانگرهای تشکیل دهنده بوده اند ولی به اشتباه آنها را به عنوان نشانگرهای انعکاسی در نظر گرفته اند. برای اینکه نشانگرها در یک روش تشکیل دهنده مدل یابی شوند باید سه نکته زیر مورد توجه قرار گیرد:دانش حقیقی یا نظری، هدف پژوهش و پیشامد تجربی در یک مدل اندازه گیری تشکیل دهنده نشانگرها به سوی متغیر مکنون هدایت شده اند که با هم به ساخت متغیر مکنون منجر می شوند. به منظور کمک در این تصمیم گیری، می توان این سؤال را پرسید که آیا تغییر در متغیر مکنون زیربنایی لزوماً منجر به تغییر مشابهی در همۀ نشانگرها خواهد شد؟ اگر پاسخ منفی باشد، نشانگرها به عنوان تشکیل دهنده یا سازنده، در نظر گرفته می شوند. اما لازم است به این نکته توجه شود که آیا مجموع نشانگرهای پیش بینی کننده، برای ساخت متغیرهای مکنون ضروری هستند؟ در این مورد، دانش حقیقی به این بررسی کمک می کند. نکته دیگر این است که آیا هدف پژوهشگر تمرکز بر سطوح انتزاعی است؟ اکر هدف پژوهشگر تبیین واریانس سطوح مؤلّفه یا متغیر غیرقابل مشاهده نسبت به نشانگرهای مشاهده شده باشد، نشانگرهای تشکیل دهنده به کار می روند. یعنی اینکه نشانگرهای یک سازه چقدر از واریانس آن سازه را تبیین می کنند. سرانجام، آیا نشانگرها از یکدیگر نسبتاً مستقل هستند؟ یعنی آیا مشکل هم خطی چندگانه بین متغیرهای مستقل وجود ندارند وحجم نمونه به اندازه کافی بزرگ است؟ اگر محقق به دنبال فهم شکل گیری متغیر مکنون باشد عدم هم خطی چندگانه بین متغیرهای مستقل مهم است و باید مورد توجه قرار گیرد. در غیر این صورت، اگر تمرکز بر رابطه های مسیر ساختاری است ممکن است عدم هم خطی چندگانه بین متغیرهای مستقل را نادیده بگیریم. شکل4-2 مثالی از روش تشکیل دهنده را نشان می دهد. در این مدل هدف تبیین واریانس نشانگرهای مشاهده شده نمی باشد، بلکه هدف افزایش واریانس تبیین شده در سطح مؤلّفه متغیر مکنون است.

شکل4-2 مدل اندازه گیری تشکیل دهنده

تفسیر متغیرهای مکنون با نشانگرهای تشکیل دهنده در هر تحلیل PLS باید بر اساس وزن ها باشد. در نهایت، بارها می تواند برای شناسایی اینکه کدام نشانگرها بهترین نماینده برای نمره مؤلّفه است محاسبه شود. استرس زندگی مثالی از مدل اندازه گیری بر اساس نشانگرهای تشکیل دهنده می باشد همان طور که در شکل 5-2 می بینیم سه نشانگر از دست دادن شغل، طلاق و مرگ یکی از اعضای خانواده به عنوان نشانگرهای تشکیل دهندۀ استرس زندگی در نظر گرفته شده اند.

شکل5-2 مدل اندازه گیری تشکیل دهنده

ویژگی های سازۀ تشکیل دهنده عبارتند از:

علّت یا ایجاد کننده متغیرهای مکنون.
نشانگرهای سازۀ تشکیل دهنده ممکن با یکدیگر دارای رابطۀ مثبت، منفی یا هیچ رابطه ای نداشته باشند.
مثال: استرس زندگی

_ از دست دادن شغل

_ طلاق

_ مرگ یکی از اعضای خانواده.

یک تفاوت عمده بین نشانگرهای تشکیل دهنده و انعکاسی این است که نشانگرهای انعکاسی باید همبستگی بالایی با همدیگر داشته باشند حال آنکه نشانگرهای تشکیل دهنده یک سازه ممکن است رابطۀ مثبت، منفی یا همبستگی صفر با یکدیگر داشته باشند.به منظور واضح شدن تفاوت بین متغیرهای تشکیل دهنده و انعکاسی هوش را به عنوان مثال بررسی می کنیم.سازۀ هوش مستقیماً قابل اندازه گیری نیست، پژوهشگران به صورت غیرمستقیم با استفاده از چندین متغیر نشانگر هوش را می سنجند.در مورد هوش، نشانگرها، نمره های به دست آمده از یک آزمون هوش می باشند. وقتی فرض شود، این نشانگرها جنبه زیر بنایی یکسانی از هوش را اندازه گیری می کنند، انعکاسی هستند. مثلاً، این وضعیت زمانی به وجود می آید که پژوهشگر هوش جبری را اندازه گیری می کند و متغیرهای نشانگر، استعداد برای جمع کردن، تقسیم و تفریق و ضرب کردن را ارزیابی می کنند. اما هنگامی که پژوهشگر بیشتر از یک جنبه از هوش را با استفاده از متغیر نشانگر اندازه گیری می کند، مثلاً هوش جبری و زبان شناختی، این متغیرهای نشانگر، تشکیل دهنده سازۀ هوش می باشند. علاوه بر مدل های اندازه گیری فوق، می توانیم یک طرح مسیر که هر دو نشانگرهای تشکیل دهنده و انعکاسی در آن استفاده می شود، داشته باشیم که به عنوان روش C نامگذاری شده است، چنین مدل هایی به عنوان انعکاس مقایسه بین افزایش پیش بینی متغیرهای مشاهده شده(روش A) و نمره های مؤلّفه های متغیر مکنون(روش B) در نظر گرفته شده اند. البته این امر ممکن است ناشی از درک نظری یا واقعی نشانگرها مانند رابطه آنها با سازه ها باشد.اما در شرایطی که دانش نظری پایین است و محقق تمایل به دنبال کردن روش C دارد، والد(1982) نشانگرهای مدل یابی برای تمام متغیرهای برون زا(مستقل) را به روش B و برای تمام متغیرهای درون زا(وابسته) به روش A پیشنهاد می کند.شکل6-2 معرّف مدل روش C دو بلوکه است. انجام تحلیل PLS بر این مدل برابر با انجام تحلیل حشو است(وان دن وولنبرگ،1977). در اینجا حشو به واریانس میانگین در بلوک *** از نشانگرها اشاره دارد که به وسیله ترکیب خطی مجموع نشانگرهای *** پیش بینی شده است.

شکل6-2 تحلیل حشو(روش C)

نکته مهم در طراحی مدل کمترین مجذورات جزئی این است که کدام روش باید در رابطۀ متغیرهای غیرقابل مشاهده با نشانگرهای تجربی استفاده شود. در این روش کمترین مجذورات جزئی(PLS) این امکان وجود دارد که نشانگرهای مشاهده شده به عنوان نشانگرهای انعکاسی یا تشکیل دهنده در نظر گرفته شوند. نشانگرهای انعکاسی مشابه با نظریه آزمون کلاسیک و مدل های تحلیل عاملی است یعنی در آنها واریانس مشاهده شذه یا کوواریانس محاسبه می شود. هر چند نشانگرهای تشکیل دهنده برای متغیرهای مشاهده شده طراحی نمی شوند، اما در مقابل برای کاهش پس ماند در رابطه های ساختاری مناسب ترین هستند.اینکه از نشانگرهای تشکیل دهنده یا انعکاسی استفاده شود تحت تأثیر روش های برآورد قرار دارد. اگر هدف یک بررسی، تبیین متغیرهای مشاهده شده است، در این صورت نشانگرهای انعکاسی بهتر است. اگر هدف تبیین انتزاعی یا واریانس مشاهده نشده است، نشانگرهای تشکیل دهنده تبیین کننده تر هستند. تصمیم گیری برای استفاده از هر یک از نشانگرهای تشکیل دهنده و انعکاسی برای یک سازه باید بر اساس ماهیت روابط علّی بین نشانگرها و متغیرهای مکنون در مدل اندازه گیری باشد. هر دو مدل تشکیل دهنده و انعکاسی می توانند در یک مدل واحد استفاده شوند. شکل7-2 مثالی از یک مدل واحد که در آن از هر دو نشانگرهای تشکیل دهنده و انعکاسی استفاده شده است، می باشد. همان طور که در شکل مشاهده می کنیم نشانگرهای متغیرهای خانه و همسالان تشکیل دهنده و نشانگرهای متغیرهای انگیزش بوده و پیشرفت تحصیلی نیز سازۀ انعکاسی می باشد.

شکل7-2 روش C با هر دو نشانگرهای تشکیل دهنده و انعکاسی

به طور کلّی، تصمیم گیری در مورد اینکه چگونه متغیرهای غیرقابل مشاهده و داده های تجربی مرتبط با یکدیگر تلقی شوند، نیازمند سه ملاحظه اساسی است: هدف مطالعه، نظریه و پیشامد تجربی. اگر هدف مطالعه تبیین واریانس های مشاهده شده است، نشانگرهای انعکاسی مناسب تر هستند. اگر هدف تبیین انتزاعی یا واریانس های غیرقابل مشاهده است، نشانگرهای تشکیل دهنده قدرت تبیین بیشتری دارند. هر دو نشانگرهای تشکیل دهنده و انعکاسی می توانند در مدل واحدی استفاده شوند. برای مثال، اگر فردی قصد دارد واریانس متغیرهای ملاک مشاهده شده از طریق متغیرهای غیر قابل مشاهده را تبیین، نشانگرهای سازۀ درون زا باید انعکاسی باشد و سازه های برون زا باید تشکیل دهنده باشد. در این صورت، نتایج برآورد روش آمیخته است. روش های A و B دو اصل مجزا را نشان می دهند. روش A نشانه واریانس های پس ماند در معادله های بیرونی و روش B کمینه ساختن واریانس های پس ماند در معادله درونی را نشان می دهد. روش C سازشی بین این دو اصل است. انتخاب نوع مدل اندازه گیری به وسیله یک جنبه از نظریه بنیادی یا ماهوی در پس مدل، یعنی روشی که کدام نوع سازۀ مکنون مفهوم سازی شده است،شکل می گیرد. سازه ای از قبیل شخصیت یا نگرش به عنوان عامل های زیربنایی که علّت نشانگرهای مشاهده شده در نظر گرفته می شوند، انعکاسی هستند. در مقابل در روش تشکیل دهنده سازه ها به عنوان ترکیب های تبیینی از نشانگرها که به وسیله ترکیب متغیرها تعیین شده اند در نظر گرفته می شوند. سرانجام، انتخاب نوع نشانگر بستگی به پیشامد تجربی دارد. در روش تشکیل دهنده، حجم نمونه و هم خطی چندگانه نشانگرها بر پایداری ضرایب آنها اثر می گذارند. زیرا این روش بر اساس رگرسیون چندگانه است. در روش انعکاسی، ضرایب نشانگر بر اساس رگرسیون ساده برآورد می شوند، بنابر این تحت تأثیر هم خطی چندگانه قرار نمی گیرند. این ملاحظات که شامل حدف مطالعه، نظریه و پیشامد تجربی هستند، ممکن است در تناقض باشند و ممکن است انتخاب نوع مدل اندازه گیری را با مشکل مواجه کنند. برای مثال فردی ممکن است بخواهد در بخش ساختاری مدل، واریانس پس ماند را کمینه سازد، که در این صورت استفاده از نشانگرهای تشکیل دهنده پیشنهاد می شود. اگر چه سازه ها به صورت مشاهده شده خود را نشان می دهند، در این صورت استفاده از نشانگرهای انعکاسی پیشنهاد می شود. در چنین مواردی تحلیل باید دوبار برآورد شود و هر بار با یک روش. اگر نتایج مطابقت داشت، مشکلی به وجود نمی آید. اما اگر نتایج متفاوت باشد در این صورت استفاده از ساختارهای عاملی بلوک ها به طور جداگانه ضرورت می یابد.

حجم نمونه

در روش PLS انتخاب حجم نمونۀ مناسب، تابع قوانین پیچیده ای است. حجم مناسب تا اندازه ای بستگی به میزان مناسب بودن ساختار عاملی و ضرایب مسیری دارد که پژوهشگر در پی آن است . مارکولیدز و سلندرز(2006) بر اساس مطالعات مشابه، جدولی را انتشار دادند که در آن حجم نمونۀ مورد نیاز با سطح مناسب توان برابر با 8/0 برای رد فرضیه صفر عدم همبستگی عامل ها در جامعه، آورده شده است. علاوه بر آن نتایج مونت کارلو تحقیق آنها نشان داد،در صورتی برآوردهای PLS در نمونه های خیلی کوچک قابل اعتماد است که بارهای عاملی بزرگ بوده و پژوهشگر همبستگی های بالایی را در عامل ها بررسی می کند. بررسی آنان نشان داد که با استفاده از نشانگرهای با بارهای عاملی7/0 و همبستگی های 2/0 برای عامل ها،حجم نمونۀ 1261 مورد نیاز است تا سطح توان 8/0 به دست آید. حجم نمونۀ 98 برای بارهای حداقل 6/0 با همبستگی های حداقل 4/0 حجم نمونۀ 23 برای بارهای حداقل 7/0 با همبستگی بین عوامل در حد حداقل 6/0 مناسب است. علاوه بر آن PLS با داده های دارای توزیع غیر نرمال، حجم نمونۀ کوچک و متغیرهای برون زای همبسته بهتر از روش مبتنی بر کوواریانس عمل می کند. همچنین با حجم نمونۀ بزرگ و داده های توزیعی نرمال، هر دو رویکرد بدون تناقض در کشف تفاوت بین گروه ها کارایی دارند. حجم نمونۀ در مدل یابی مسیر PLS می تواند تا اندازه قابل ملاحظه ای کوچک باشد. برای نمونه متغیرها نسبت به مشاهده ها بیشتر بوده و ممکن است مقداری از داده ها به طور تصادفی به دست نیامده باشد. به دلیل این ویژگی هاست که محققان، هنگامی که حجم نمونه نسبتاً پایین است از مدل سازی مسیر PLS به جای لیزرل استفاده می کنند.انتخاب حجم نمونۀ مناسب بیشتر به اندازه روابط یا سطح توان دلخواه وابسته است. پژوهشگر قبل از تصمیم گیری برای انتخاب یک نمونه مناسب باید ویژگی های توزیعی داده ها، داده های حاصل نشده بالقوه ، ویژگی های سنجش متغیرهای مورد بررسی و مقدار روابط را مورد توجه قرار دهد، یا اطمینان یابد که واقعاً حجم نمونۀ کافی برای مطالعۀ پدیده مورد علاقه در دسترس است. با وجود اینکه PLS برای نمونه های خیلی کوچک و یا موقعی که مورد نسبت به متغیرهای نشانگر کمتر باشد قابل استفاده است،اما تکیه بر نمونه های کوچک می تواند نتایج ضعیفی فراهم کند. نمونه های بزرگتر، برآوردهای PLS را قابل اطمینان تر می سازد. بنابراین میانگین میزان خطای مطلق در PLS با افزایش حجم نمونه کاهش می یابد. حجم نمونۀ کوچک برای ضرایب مسیر کوچک کافی نیست، در این صورت حجم نمونۀ برابر با مدل یابی معادلات ساختاری مورد نیاز است. در واقع برخی از متخصصین توصیه می کنند استفاده کنندگان PLS از راه برد”قاعده 10″ مشابه با مدل یابی مبتنی بر کوواریانس استفاده کنند. یعنی تعداد ده مورد برای هر متغیر اندازه گیری شده نیازمند است. متخصصان پیشنهاد می کنند که انتخاب حجم نمونه در روش PLS براساس قواعد زیر باشد:

ده برابربیشتر از تعداد نشانگرهای تشکیل دهنده یک سازه باشد.
ده برابر بیشتر از تعداد مسیرهای ساختاری جهت دار در یک سازۀ خاص در مدل ساختاری باشد.

یعنی در یک مدل تشکیل دهنده، سازه ای که دارای بیشترین تعداد نشانگرهای تشکیل دهنده است را شناسایی نموده و این تعداد را ده برابر می کنیم تا حجم نمونه به دست آید. در مدل انعکاسی نیز متغیر مکنون وابسته ای که بیشترین مسیر به سمت آن نشانه رفته را مشخص نموده و تعداد این مسیرها را ده برابر نموده تا حجم نمونه را به دست آوریم. البته قاعده دیگر این است که در مدل انعکاسی، سازه ای که دارای بیشترین نشانگرهای انعکاسی است را مشخص نموده و تعداد این نشانگرها را ده برابر نموده تا حجم نمونه را به دست آوریم.

پیچیدگی مدل

بعضی توابع ناهمخوانی مدل یابی معادلات ساختاری مبتنی بر کوواریانس( یعنی (یعنی GFI و AGFI) پیچیدگی مدل، یعنی سازه ها یا متغیرهای مشاهده شده بیشتر را کاهش می دهند و این توابع ممکن است برای مدل های پیچیده تر نامناسب باشند. برای مثال، پژوهشگران به صورت آزمایشی پیچیدگی مدل یعنی تعداد پارامترهای برآورده شده و تعداد درجه آزادی را تغییر دادند، و به این نتیجه رسیدند که با افزایش پارامترهای برآورد شده، ناهمگرایی و راه حل های نامناسب بیشتری نیز اتفاق می افتد. با این حال، حجم نمونه اثر اصلی دارد. با افزایش تعداد مشاهده ها، ناهمگرایی و راه حل نامناسب کاهش می یابد. در همین راستا، به اعتقاد برخی از متخصصان اگر حجم نمونه و بارهای عاملی تقریباً یکسان باشند، ناهمگرایی و را حل های نامناسب به انداره پیچیدگی مدل افزایش می یابد(وینزی و همکاران،2010). در عمل، محققان اغلب ویژگی های مدل و داده ها را پیش از گرآوری و تحلیل داده ها نمی دانند. در حوضه های جدید پژوهش های کاربردی، به ویژه موقعی که ابزارهای اندازه گیری در مرحله ساخت هستند، ویژگی های توزیعی متغیرهای مشاهده شده نامعلوم است.همچنین در مرحله کشف مدل، پیچیدگی مدل نهایی، تعداد نشانگرهای قابل اعتماد و اندازه بارهای عامل نا مشخص است. پیداست که با اندازه گیری بهتر و بنیادهای نظری قوی تر از ساختارهای مدل، آسان تر می توان تصمیم های مناسبی برای انتخاب برآورد کننده ها و حجم نمونه گرفت. این موارد بر ویژگی تکمیلی PLS در رابطه با مدل یابی معادلات ساختاری مبتنی بر کوواریانس در آزمون نظریه، به ویژه موقعی که مدل پیشرفت هایی از ساده به مدل های پیچیده تر دارد، تأکید می کنند.در واقع PLS برای تبیین مدل های پیچیده تر مناسب است، زیرا الگوریتم PLS امکان افزایش پیچیدگی قابل توجهی در مدل را فراهم می کند.

مقاوم بودن یا خدشه ناپذیری برآوردهای پارامتر

محققان به اطلاعات خدشه ناپذیری برآورد پارامترها هنگامی که یک وسیله مناسب برای برآورد مدل یابی معادلات ساختاری خاص از داده های گردآوری شده انتخاب می کنند. نیاز دارند. ویلارز، آلمیدا و کولهو(2009) در یک مطالعۀ شبیه سازی اوّلیّه مونت کارلو اثرات دو فرض را بر عملکردCBSEM وPLS تحلیل کردند:تقارن توزیع و مدل یابی انعکاسی نشانگرها. این محققان نتایج هر دو روش را هنگام رعایت و عدم رعایت این فرض ها، بررسی کرده اند. برای نمونه، هنگامی که توزیع مشاهده ها چولگی دارد و بعضی نشانگرها بر اساس الگوی تشکیل دهنده شکل گرفته اند، کیفیت دو روش برآورد به ویژه برای برآورد بارهای بیرونی خیلی مشابه است. مطالعۀ ویلارز و همکاران(2009) از این نکته که در PLS بارهای بیرونی بیشتر برآورد می شد و نتایج محافظه کارانه ای برای روابط مدل مسیر درونی ایجاد می شود حمایت می کند. در صورتی که بیشینه درست نمایی با بیش برآورد ضرایب مسیر و کم برآورد بارهای نشانگر دقیقاً گرایش معکوسی دارد،. در شرایطی که یک متغیر مکنون تشکیل دهنده وجود دارد، روش PLS نیرومندی بیشتر در مقایسه با CBSEM نشان می دهد. بنابراین، محققان در مورد داده های دارای چولگی نتیجه می گیرند که برآوردهای PLS نسبت به برآوردهای بیشینه درست نمایی بر حسب اریب و دقت، بهتر است. به نظر می رسد برآورد کننده بیشینه درست نمایی به ایرادهای متنوع در داده ها و ویژگی های مدل حساس ترباشد. به طور کلّی، برآوردهای پارامترPLS نسبت به اریب و همسانی کمتر، بهینه هستند. برآوردها در شرایط همسانی بزرگ یعنی حجم نمونۀ بزرگ و تعداد زیاد نشانگرهای هر متغیر مکنون، به صورت مجانب درست خواهند بود.

الگوریتم PLS

همان طور که ذکر شد، دو رویکرد برای برآورد پارامترهای یک مدل معادلات ساختاری وجود دارد، که شامل رویکرد مبتنی بر کوواریانس و رویکرد مبتنی بر واریانس یا PLS می باشد. رویکرد مبتنی بر کوواریانس سعی در کاهش تفاوت بین کوواریانس نمونه و کوواریانسی که توسط مدل نظری پیش بینی شده است، دارد. بنابراین فرآیند برآورد پارامترها سعی دارد تا کوواریانس ماتریس مقادیر مشاهده شده را دوباره تولید کند(هومن، 1387). بر خلاف رویکرد مبتنی بر کوواریانس، PLS در ابتدا توسط هرمن والد(1975) تحت عنوان NIPALIS ( حداقل مجذورات جزئی از سرگیرنده غیر خطی) معرّفی گردید.این رویکرد به جای بازتولید ماتریس کوواریانس تجربی، بر بیشینه سازی واریانس متغیرهای وابسته که توسط متغیرهای مستقل پیش بینی می شوند، تمرکز دارد. این رویکرد همانند رویکرد لیزرل، از بخش ساختاری که نمایانگر روابط بین متغیرهای پنهان، و بخش اندازه گیری که نشانگر روابط متغیرهای پنهان با نشانگرهایشان است، تشکیل شده است. در رویکرد PLS بخش ساختاری، مدل درونی و بخش اندازه گیری مدل بیرونی نام دارد. اما رویکرد PLS علاوه بر این دو بخش دارای بخش سومی نیز می باشد، که نسبت های وزنی نام دارد. این بخش جهت برآورد مقادیر موردها یا نمرات عاملی برای متغیرهای پنهان مورد استفاده قرار می گیرد(نمرات افراد در متغیرهای مکنون) (چین، 1998). بر خلاف رویکرد مبتنی بر کوواریانس که ابتدا پارامترهای مدل برآورد شده و سپس مقادیر موردها از طریق برکشت دادن آنها به مجموعه تمام نشانگرها، برآورد می شود، مانند مقادیر برآورد شده برای هر متغیر پنهان در هر مجموعه از داده ها، در رویکرد PLS ابتدا مقادیر موردها محاسبه می شود. برای نیل به این مقصود، متغیرهای پنهان به صورت ترکیب دقیق خطی نشانگرهای تجربی خود برآورد می شوند(فرنل و بوکشتان،1982). سپس PLS از این نمایندگان برآورد شده به عنوان جانشین های کاملی برای متغیرهای پنهان استفاده می کند(هین لاین و کاپلان،2004). وزن های مورد استفاده برای تعیین مقادیر موردها به صورتی محاسبه می شوند که بیشترین واریانس مفید برای پیش بینی متغیرهای وابسته از روی متغیرهای مستقل را شامل شود. این امر بر این فرض استوار است که تمامی واریانس اندازه گیری شدۀ متغیرها در مدل، واریانس مفیدی هستند که باید تبیین شوند(چین، مارکولین و نیوستد،1996). این بخش از تحلیل PLS به تحلیل عاملی مؤلّفه های اصلی شباهت دارد که تمامی واریانس متغیرهای اندازه گیری شده را تحلیل نموده و عوامل را به صورت ترکیب خطی ساده نشانگرها برآورد می کند. اما در رویکرد لیزرل که بر اساس تحلیل عوامل مشترک قرار دارد، فقط واریانس مشترک تحلیل شده و به صورت ضمنی بین نشانگرها، عوامل زیربنایی و خطاهای اندازه گیری تمایز قائل می شود(کلاین،2011). پس از محاسبه وزن ها در رویکرد PLS این امکان فراهم می شود تا مقادیر هر متغیر پنهان تعیین شود. این امر به وسیله محاسبه میانگین وزنی نشانگرهای یک سازه انجام می گیرد. پس از محاسبه مقادیر متغیرهای پنهان، وزن های مسیر ساختاری از طریق رگرسیون حداقل مجذورات معمولی OLS محاسبه می شود. شایان ذکر است که این الگوریتم تا زمان رسیدن به همگرایی و کسب نتیجه مطلوب تکرار می شود(هین لاین و کاپلان،2004). با توجه به مطالبی که ذکر گردید، ایده اساسی PLS سر راست و ساده به نظر می رسد: در ابتدا، نسبت های هم وزنی که نشانگرها را به متغیرهای پنهان مورد نظرشان مربوط می کند، برآورد می شود، سپس، با در نظر گرفتن نسبت های وزنی به عنوان ورودی، مقادیر موردها برای هر متغیر پنهان بر اساس میانگین وزنی نشانگرهایش محاسبه می شود. در نهایت از این مقادیر موردها در معادلات رگرسیون استفاده شده تا پارامترهای روابط ساختاری تعیین شود(فرنل و بوکشتاین،1982). با توجه به مطالبی که ذکر شد می توان نتیجه گرفت که مهمترین قسمت تحلیل PLS، برآورد نسبت های وزنی می باشد. البته شاید این فکر به ذهن برسد که می توان برای تمامی نشانگرها وزن برابری را در نظر گرفت،اما این امر دو مشکل اساسی دارد:نخست، هیچ تبیین نظری و منتقی وجود ندارد که تمامی نشانگرها وزن یکسانی داشته باشند. زیرا در این صورت پارامترهای برآورد شدۀ مدل ساختاری بر اساس نوع وزن دهی تغییر می کند که این امر نیز در موجب کسب نتایج قراردادی و دل بخواهی می شود(هین لاین و کاپلان،2004). دیگر اینکه، همان طور که چین و نیوستد(1999) تأکید می کنند، این راه حل این واقعیت را نادیده می گیرد که بعضی از معرّف ها در مدل دارای پایانی بیشتر نسبت به معرّف های دیگر هستند، بنابراین این معرّف ها وزن های بیشتری می گیرند. با توجه به این مطالب، رویکرد PLS از فرآیند دو مرحله ای برآورد پیچیده تری برای تعیین وزن ها(w_i) استفاده می کند. در ابتدا، تخمین بیرونی صورت می گیرد. در این مرحله، مقادیر موردهایی هر متغیر مکنون مانند ****** در مدل نظری شکل 1، بر اساس میانگین وزنی نشانگرهای خود برآورد می شود ((******=w1y3 + w2 y4. برای تعیین این وزن ها در مدل های انعکاسی از تحلیل مؤلفّه های اصلی استفاده شده و در مدل های تشکیلی از تحلیل رگرسیون استفاده می شود(کاسل، هاکل، وستلاند، 1999). در مرحله بعدی،تخمین درونی صورت می گیرد. در این مرحله نمرات موردهای بهبود یافته از طریق میانگین وزنی متغیرهای پنهان مجاور تعیین می شود.(***********************************).برای حصول نتیجه در این مرحله، سه طرح مختلف وزن دهی در دسترس است(سنتروئید یا مرکز ثقل، عاملی و طرح وزن دهی مسیر). والد(1982) طرح اصلی سنتروئید یا مرکز ثقل را ارائه داد و لوهمولر(1989) نیز طرح های وزن دهی عاملی و مسیر را ارائه داد. طرح سنتروئید از علامت همبستگی های بین یک متغیر مکنون و متغیرهای مجاور آن استفاده می کند. طرح وزن دهی عاملی از همبستگی ها استفاده می کند و طرح وزن دهی مسیربه جهت مسیرها در مدل مسیر توجه می کند.شایان ذکر است که انتخاب هر یک از این طرح های وزن دهی فقط تأثیر اندکی در نتایج نهایی دارد، اما متخصصان استفاده از طرح وزن دهی مسیر را به خاطر اینکه این طرح تنها طرح برآوردی است که به صراحت جهت ارتباطات مسیر پیش بینی معیّن را در نظر می گیرد،پیشنهاد می کنند(وینزی و همکاران، 2010).با استفاده از برآورد ثانویه مقادیر موردها،نسبت های وزنی تغییر پیدا می کند(**********************) فرآیند تخمین بیرونی و درونی تا زمانی تکرار می شود که همگرایی مقادیر موردها به دست آید. سپس بارهای عاملی و ضرایب رگرسیون محاسبه می شوند.همچنین برای محاسبه ضرایب مسیر هر متغیر مکنون درون زا از رگرسیون خطی چندگانه استفاده می شود(کاسل و همکاران،1999). هنگامی که هدف، کاربرد و پیش بینی است رویکردPLS مناسب است.همان گونه که گفته شد مطابق با این رویکرد، فرض این است که تمام واریانس مورد اندازه گیری، برای تبیین به کار می رود. از آنجایی که در این رویکرد متغیرهای مکنون به عنوان ترکیب خطی دقیقی از اندازه گیری های مشاهده شده برآورد می شوند از مشکل عدم تعیین جلوگیری می شود و تعریف دقیقی از نمره های مؤلّفه فراهم آورده می شود. با استفاده از روش برآورد سرگیری(والد، 1982)، PLS مدل کلّی فراهم می کند که همۀ روش های دیگر همبستگی بنیادی، رگرسیون چندگانه، تحلیل واریانس چند متغیره و مؤلّفه های اصلی را شامل می شود. به دلیل اینکه الگوریتم از سرگیری از مجموعه تحلیل های کمترین مجذورات متداول تشکیل شده است، شناسایی مدلهای بازگشتی مشکل نیست و هیچ مفروضه ای در مورد شکل توزیع متغیرهای اندازه گیری شده ضرورت ندارد.

ویژگی پیش بینی کننده

ویژگی اساسی مدل سازی PLS ویژگی پیش بینی کننده است. در حالی که برآوردهای مبتنی بر کوواریانس بر فرض های مشترک ویژه توزیع چند متغیری و استقلال مشاهده ها وابسته است، رویکرد PLS این فرض های سخت گیرانه را ندارد. در عوض، روش مدل یابی PLS، فرض های توزیعی نرم دارد که باعث شده این رویکرد به مدل یابی نرم معروف شود.همان گونه لوهمولر(1989) اظهار می کند، روش های برآورد مدل ها و مفاهیم نرم نیستند بلکه تنها فرض های توزیعی نرم هستند. ویژگی پیش بین بر رابطه هایی که پژوهشگران می خواهند برای پیش بینی استفاده کنند تأثیر می گذارد، ویژگی پیش بین، به صورت برآورد شده یا نظری، امکان پیش بینی های بعدی را فراهم می کند. علاوه براین لوهمولر(1989) بیان می کند که: ویژگی پیش بین با هدف پیش بینی نه یک تبیین ساختاری، هنگامی که هدف پیش بینی به خطر انداختن تفسیر علّی _ ساختاری از رابطه نباشد، سیستمی از رابطه های خطی بهتری را تدوین می کند. در واقع ویژگی پیش بین به پژوهشگران این امکان را می دهد که در مدل آزمون شدۀ خود به عنوان ابزاری برای پیش بینی در دنیای واقعی استفاده کنند. عمل پیش بینی از طریق نمره های عاملی افراد در هر یک از متغیرهای مکنون صورت می گیرد. در ادامه با توجه به مطالبی که ذکر شد توضیح مختصری در مورد ویژگی ها، مشخصات مدل مسیر PLS ، مزایا ومعایب کمترین مجذورات جزئی بیان خواهیم کرد.

ویژگی های روش PLS

ویژگی های PLS عبارتند از:

PLS نمره های متغیرهای مکنون یعنی سازه ها را که از طریق یک یا چندین نشانگر یا متغیرهای آشکار اندازه گیری می شوند، برآورد می کند.
مدل یابی مسیر PLS هنگامی که حجم نمونه کوچک باشد قابل کاربرد است. بنابراین در موقعیت هایی که نمی توان از روش های دیگر استفاده کرد قابل کاربرد است.
مدل یابی مسیر PLS توان برآورد مدل های پیچیده با متغیرهای مکنون و آشکار زیادی را دارد.
مدل یابی مسیر PLS فرض های سخت گیرانه کمتری درباره توزیع متغیرها و خطا دارد.
PLS با هر دو نوع مدل اندازه گیری تشکیل دهنده و انعکاسی به کار می رود.

البته باید توجه کرد که در مورد ویژگی های مدل یابی مسیر PLS بحث هایی وجود دارد، از جمله مدل یابی مسیر PLS فرض های سخت یا دقیق درباره معرّف بودن نمونه ندارد. بعضی اوقات مدل یابی مسیر PLS تنها روشی است که می تواند با نشانگرهای تشکیل دهنده عمل کند. اگر چه مقایسه روش ها نشان می دهد که PLS هنگام مشکل هم خطی چندگانه خوب عمل می کند، اما این مشکل را رفع نمی کند. پژوهشگران مهم ترین انگیزه استفاده از PLS را اکتشاف و پیش بینی بیان می کنند. متخصصان، مدل یابی مسیر با استفاده از PLS را در مراحل اوّلیّه توسعه نظری به منظور آزمون و معتبر ساختن مدل های اکتشافی پیشنهاد می کنند. اکنون که روش های مورد استفاده برای PLS را توضیح دادیم، می توانیم خصوصیات مدل رسمی که این فرآیند را هدایت می کند، معیّن کنیم. همۀ متغیرهای مکنون مدل های مسیر در PLS سه مجموعه از رابطه ها را شامل می شوند: 1) مدل درونی(مدل ساختاری) که رابطۀ بین متغیرهای مکنون را مشخص می کند 2) مدل بیرونی(مدل اندازه گیری) که رابطۀ بین متغیرهای مکنون را با متغیرهای آشکار و مشاهده شده مشخص می کنند 3) رابطه های وزنی فوق که ارزش های مورد برای متغیرهای مکنون برآورد می شوند.

مزایای اصلی کمترین مجذورات جزئی عبارتند از:

چندین متغیر مستقل و وابسته را به صورت همزمان تبیین می کند.
امکان دست کاری هم خطی چندگانه متغیرهای مستقل را فراهم می کند.
با وجود داده های پارازیت و داده های حاصل نشده توان آماری بالایی دارد.
بررسی متغیرهای مکنون تشکیل دهنده و انعکاسی را ممکن می سازد.
با نمونه های کوچک به کار می رود.
وابسته به توزیع نیست.
با داده های اسمی، ترتیبی و پیوسته به کار می رود.

بعضی از معایب کمترین مجذورات جزئی عبارتند از:

در تفسیر بارهای متغیرهای مکنون مستقل با دشواری مواجه است.
ویژگی های توزیعی برآوردها مشخص نیست.
آزمون معناداری ندارد مگر با اجرای بوت استراپ یا برش متقاطع.
عدم وجود شاخص های آماری آزمون مدل به جز یک شاخص GOF یا شاخص برارزش مدل.

فصل سوم: طراحی و آزمون مدلPLS

مقدمه

آزمون مدل PLS همانند مدل یابی مبتنی بر کوواریانس از دو قسمت آزمون مدل اندازه گیری و مدل ساختاری تشکیل یافته است. در قسمت آزمون مدل اندازه گیری به بررسی روایی و پایانی ابزارها پرداخته می شود و در قسمت آزمون مدل ساختاری فرضیه های تحقیق و برازش مدل مورد بررسی قرار می گیرد. پس از طراحی مدل نظری در کاربرد PLS سه مجموعه کلّی از موضوعات روش شناختی باید مورد توجه قرار گیرد:1) ارزیابی روایی و اعتبار اندازه گیری ها، 2) تعیین روابط مناسب بین اندازه گیری ها و سازه ها 3) تفسیر ضرایب مسیر،بسندگی مدل تعیین شده و انتخاب مدل نهایی که در این فصل به توضیح آنها می پردازیم.

طراحی الگو در مدل مسیر

در مدل مسیر PLS پژوهشگران با طراحی مدل مفهومی شروع می کنند.شکل1-3 یک مدل مفهومی را نشان می دهد.اصل اساسی در PLS این است که همۀ اطلاعات راجع به روابط بین K از بلوک متغیرهای مشاهده شدۀ

X₁,X_2,…..,X_k فرض شده، از طریق k متغیرZ_1,Z_2,….,Z₃ منتقل شود. متغیر مکنون Z_k متغیر غیرقابل مشاهده است که به صورت غیرمستقیم توسط بلوک P_kمتغیرهای قابل مشاهدهX_k = [X_k, ₁X_{k, 2}^….X_{k, pk}] توصیف می شود. K بلوک از متغیرهای آشکارX_1,X_2,…..,X_k با نمونه های یکسانی اندازه گیری می شود.

شکل1-3 مدل مفهومی با پنج بلوک از نشانگرها

هنگام ترسیم گرافیکی مرسوم از مدل مفهومی، متغیرهای آشکار با مربع و متغیرهای مکنون با دایره نشان داده می شوند. با استفاده از بصیرت و دانش پیشین، محقق آزاد است تا ارتباط بین متغیرهای مکنون را مشخص کند. هنگامی که فرض بر این است که متغیرهای مکنون با هم مرتبط هستند، باید تبیین شود که آیا متغیرهای مکنون با متغیرهای دیگر مرتبط هستند یا نه؟ همچنین آیا متغیرهای مکنونی که به عنوان متغیرهای برون زا در نظر گرفته می شوند یعنی هرگز به عنوان متغیرهای وابسته ظاهر نمی شوند و متغیرهایی که به عنوان درون زا در نظر گرفته می شوند، یعنی به عنوان متغیرهای وابسته ظاهر می شوند، با یکدیگر ارتباط دارند یا نه؟ شکل1-3 نمونه ای از مدل مفهومی با 5بلوک را نشان می دهد.متغیرهای مکنونZ₁_وZ₂ برون زا بوده و متغیرهای دیگر درون زا می باشند. در این شکل دو نوع مدل را می توان در نظر گرفت: اوّلین مدل، مدل اندازه گیری است که در آن متغیرهای آشکار با متغیرهای مکنون مربوط به خود مرتبط می شوند. در این مدل هر کدام از متغیرهای آشکار با یک مدل رگرسیون ساده سه متغیری با متغیرهای مکنون مرتبط است. دومین مدل، مدل ساختاری است. در مدل ساختاری متغیرهای مکنون با دیگر متغیرهای مکنون مرتبط می شوند. متغیر مکنونی که هرگز به عنوان متغیر وابسته ظاهر نمی شود، متغیر برون زا و در غیراین صورت درون زا نامیده می شوند. در مدل ساختاری هر کدام از متغیرهای مکنون برون زا با متغیرهای مکنون دیگر از طریق مدل رگرسیون چندگانه مرتبط هستند. به طور کلّی گام ها برای انجام یک مطالعه با استفاده از کمترین مجذورات جزئی(PLS) به شرح زیر است:

رسم نمودار مسیر.

الف. فالک و میلر توصیه می کنند از روش نمودار مدل یابی فعال شبکه ای استفاده کنیم.

ب. بر این اساس 1) سازه های نظری= متغیرهای مکنون= دایره ها 2) متغیرهای اندازه گیری شده= مربع ها 3) رابطه های نا متقارن= پیکان نوک دار دو طرفه.

معرّف های نوموگرافیک در کمترین مجذورات جزئی

همانندمدل یابی معادلات ساختاری، کمترین مجذورات جزئی مزایایی اضافه بر فراهم کردن نمایش گرافیکی روابط بین متغیرها دارد. یک مثال از این نوع برون داد به شرح ذیل است:

شکل 2-3 مثالی از مدل مسیر PLS با نشانگرهای انعکاسی و تشکیل دهنده

چهار ویژگی نمودار:

مرتب کردن سازه های نظری.
تعیین پیکان ها.
تعیین مدل درونی.
بلوک بندی متغیرهای نظری و آشکار و تعیین نمودن جهت هایشان.

قواعد کلّی تفسیر:

وجود حداقل سه متغیر آشکار برای یک متغیر مکنون.
بارهای مسیرهای بین مؤلفّه ها و متغیرهای آشکار باید بیشتر از 55/0 باشد.
واریانس تعیین شده برای متغیرهای درون زا باید بیشتر از 10/0 باشد.

آزمون مدل اندازه گیری (مدل انعکاسی)

روایی و اعتبار

اگرچه PLS پارامترها را برای هر دو نوع رابطۀ بین اندازه گیری ها و سازه ها(بارها) و ارتباط بین سازه های متفاوت(ضرایب مسیر) به صورت همزمان برآورد می کند، مدل PLS معمولا در دو مرحله متوالی تحلیل و تفسیر می شود: 1) ارزیابی روایی و اعتبار مدل اندازه گیری 2) ارزیابی مدل ساختاری. این توالی برای اطمینان از آن است که پژوهشگر اندازه گیری های پایا و روا از سازه ها قبل از نتیجه گیری درباره ماهیت رابطۀ سازه ها داشته باشد. بسندگی مدل اندازه گیری با جستجو در 1) اعتبار گویه های انفرادی 2) روایی همگرا از اندازه گیری های مرتبط با سازه های فرعی و 3) روایی تشخیصی ارزیابی می شود.

اعتبار گویه

در PLS اعتبار گویۀ انفرادی با بررسی بارها یا همبستگی ساده اندازه گیری ها در سازه های مربوط به خودشان ارزیابی می شود. یک قاعده کلّی که به وسیله بسیاری از پژوهشگران به کار می رود پذیرش گویه ها با بارهای دست کم 7/0 است،که اشاره به بیشترین واریانس مشترک بین سازه ها و اندازه هایشان نسبت به واریانس خطا است. از آنجایی که بارها همان همبستگی ها هستند، بدین معنی است که بیش از 50 درصد واریانس در متغیر مشاهده شده ناشی از سازه باشد. در عمل به طور متداول، ممکن است حداقل چندین گویۀ اندازه گیری شده وجود داشته باشد که در یک مدل دارای بارهای زیر آستانه 7/0 باشند، به ویژه موقعی که گویه های جدید یا مقیاس های نو به کار می رود.بار های پایین ممکن است ناشی از موارد زیر باشد:1) عبارت پردازی ضعیف یک گویه 2) نا مناسب یا نامربوط بودن گویه 3) انتقال گویه ها و اجرای آنها بدون توجه به بافت. اوّلین مشکل به اعتبار پایین، دوّمین مشکل به روایی محتوا و سازۀ ضعیف و سوّمین مشکل به عدم توانایی تعمیم دهی به بافت و موقعیت های دیگر منجر به می شود. حتی موقعی که پژوهشگر توجیه نظری قوی برای چنین گویه هایی در مدل اش دارد، گویه هایی با بارهایی خیلی پایین باید به دقّت مورد تجدیدنظر قرارگیرند، از آنجایی که آنها قدرت تبیین خیلی پایین به مدل اضافه می کنند سبب می شوند برآوردهای پارامترهای مرتبط با سازه ها ضعیف گردند. به طور کلّی گویه های با بارهای کمتر از4/0 یعنی آستانه ای که معمولاً برای نتایج تحلیل عاملی استفاده می شود یا 5/0 باید حذف شوند( هیر و همکاران، 2006).

روایی همگرا

محققان با استفاده از PLS معمولاً یک یا هر دو شاخص روایی همگرا را گزارش می کنند. این شاخص ها آلفای کرونباخ و اندازه گیری همسانی درونی یا پایایی ترکیبی که بوسیله فرنل و لارکر(1981) توسعه یافت، هستند.فرنل و لارکر اظهار می کنند که شاخص پایایی ترکیبی آنان نسبت به آلفا برتری دارد. زیرا از بارهای گویۀ به دست آمده در درون شبکه های مدل علّی استفاده می شود.بنابراین شاخص پایایی ترکیبی هنگام محاسبه از بارهای عاملی گویه ها استفاده می کند، اما ضریب آلفای کرونباخ وزن برابری به گویه ها می دهد و پایایی را کمتر نشان می دهد(مانوئل و همکاران،2009). با این وجود، تفسیر ارزش های به دست آمده مشابه است و رهنمودهای پیشنهاد شده توسط نونالی و برن اشتاین(1996) برای هر دو اقتباس می شود. بویژه آنها مقدار7/0 را به عنوان معیاری معتدل برای اعتبار مرکب پیشنهاد می کنند که در مراحل اوّلیه تحقق قابل کاربرد است. اگر چه امکان محاسبه آلفای کرونباخ برای سازه های فردی در هر مدل مورد بررسی وجود دارد، اما ارزش های همسانی درونی با استفاده از بارهای گزارش شده و فرمول پایایی ترکیبی فرنل و لارکر تعیین می شود. اعتبار مرکب به صورت زیر محاسبه می شود:*************************************** **** معرّف بار عاملی یک نشانگروVar(***)=1-**** یا بار عاملی همان نشانگر منهای یک است. همسانی درونی پایین از علل زیربنایی متنوعی نتیجه می شود از جمله تعریف ضعیف سازه یا چند بعدی بوده ، اما از طریق گویه هایی که با سازه های تک بعدی مرتبط اند اندازه گیری شود، در این صورت ، اندازه گیری ها همسانی درونی ضعیفی را نشان خواهند داد.اگر بعضی از گویه های اندازه گیری شدۀ انفرادی، بارهای عاملی بسیار قوی با سازۀ مورد نظر داشته باشند، پژوهشگر باید به فکر تقسیم کردن سازۀ اصلی به سازه های جدید، هر کدام با نشانگرهای خودشان، یا حذف گویه ها برای ایجاده سازۀ تک بعدی بیافتد. برای نمونه اگر ساختار سازمانی به عنوان یک سازۀ چند بعدی ظاهر شود، به منظور حل این مشکل، او باید بعضی از گویه ها یا نشانگرها را حدف کند یا سازه را به دو زیر سازه بخش بندی کند.

روایی تشخیصی

روایی تشخیصی، مکملی برای روایی همگرا است، که نشان دهندۀ میزان تمایز نشانگرهای یک سازۀ معیّن از نشانگرهای سازنده های دیگر در مدل یکسان است.در مدل یابی PLS، یک معیار برای مناسب بودن روایی تشخیصی این است که سازه باید بیشترین واریانس مشترک را با نشانگرهایش نسبت به اشتراک آن با سازه های دیگر در یک مدل معیّن داشته باشد. برای ارزیابی روایی تشخیصی، فرنل و لارکر(1981) استفاده از میانگین واریانس استخراج شده AVE یعنی، میانگین واریانس مشترک بین سازه و نشانگرهایشان را پیشنهاد می کنند. با فرض نشانگرهای استاندارد شده و برآوردهای متغیرهای مکنون AVE به صورت زیر محاسبه می شود:****************************************** ***** معرّف بارهای مؤلّفه با یک نشانگر و ********************* است. فرنل و لارکر(1981) مقادیرAVE 5/0 و بیشتر را توصیه می کنند و این امر به معنای آن است که سازۀ مورد نظر حدود 50 درصد و یا بیشتر واریانس نشانگرهای خود را تبیین می کند. میانگین واریانس استخراج شده باید از واریانس مشترک آن سازه و سازه های دیگر موجود در مدل، یعنی همبستگی بین دو سازه، بیشتر باشد. در ماتریس همبستگی، همبستگی بین سازه های متفاوت در عناصر غیرقطری چپ ماتریس و جذر میانگین واریانس استخراج شده برای هر سازه در امتداد خط قطری نشان داده می شود. برای مناسب بودن روایی تشخیصی، عناصر قطری به صورت معناداری باید از عناصر غیرقطری در ستون ها و سطرها بیشتر باشد. جدول 1-3 همبستگی میان متغیرها و جذر میانگین واریانس استخراج شده را نشان می دهد. میانگین واریانس استخراج شده در جدول پر رنگ تر شده است که نشان می دهد همبستگی هر سازه با نشانگرهای خود بیشتر از همبستگی اش با سازه های دیگر است.

جدول 1-3 همبستگی میان متغیرها و میانگین واریانس استخراج شده

علاوه بر معیار فوق گیفن و اشتراپ(2005) توصیه می کنند که گویه های یک سازه باید بیشترین بار عملی را بر سازۀ خود داشته باشند. یعنی بار مقطعی کمی بر سازه های دیگر داشته باشند. آنها پیشنهاد می کنند که بار عاملی هر گویه بر روی سازۀ مربوط به خود باید حداقل 1/0 بیشتر از بار عاملی همان گویه بر سازه های دیگر باشد. در جدول 2-3 نتایج این معیار نشان داده شده است.

جدول2-3: بار عاملی و بار مقطعی هر یک از گویه ها بر سازه ها

همان طور که در جدول فوق مشاهده می کنید نشانگرهای یک سازه بیشترین بار عاملی را بر سازۀ مورد نظر خود و کمترین بار را بر سازه های دیگر دارند.

شاخص اشتراک

شاخص اشتراک، کیفیت مدل اندازه گیری هر بلوک را اندازه می گیرد. این شاخص برای هر بلوک j به صورت زیر تعریف می شود. ********************************* میانگین اشتراک نیز میانگین تمامCor²(X_jh,Y_j) می باشد.******************************** که در این معادله P کل تعداد متغیرهای مشاهده شده در تمام بلوک ها می باشد. شاخص اشتراک نوعی شاخص بررسی برارزش مدل اندازه گیری یک بلوک یا متغیر مکنون است.مقادیر مثبت این شاخص نشانگر کیفیت مناسب مدل اندازه گیری می باشد. از میانگین شاخص اشتراک نیز می توان برای برازش کلّی مدل اندازه گیری استفاده نمود. تفسیر این شاخص نیز همانند شاخص اشتراک می باشد. به صورت خلاصه مدل انعکاسی بدین صورت ارزش یابی می شود. اولّین معیاری که معمولاً بررسی می شود همسانی درونی است. معیار سنتی برای همسانی درونی آلفای کرونباخ است که برآوردی از اعتبار مقیاس یا سازه را بر اساس همبستگی متقابل نشانگرها فراهم می کند. در آلفای کرونباخ فرض بر این است که همۀ نشانگرها اعتبار برابری دارند، اما PLS نشانگرها را مطابق با اعتبار آنها اولویت بندی می کند. در این صورت آلفای کرونباخ برآوردهای پایین تری از اعتبار همسانی درونی متغیرهای مکنون در مدل مسیر PLS فراهم می کند. در این صورت بهتر است که از اعتبار مرکب استفاده کنیم. مفروضه اعتبار مرکب این است که نشانگرها بارهای متفاوتی دارند. این شاخص مشابه با آلفای کرونباخ تفسیر می شود. در مراحل اوّلیّه تحقیق اعتبار همسانی درونی بالای 7/0 و 9/0 و در مراحل بعدی ارزش بالای 8/0 رضایت بخش است. در صورتی که این مقدار زیر 6/0 باشد، عدم اعتبار سازه را نشان می دهد. در PLS باید اعتبار هر کدام از نشانگرها نیز ارزیابی شود. محققان فرض می کنند که متغیر مکنون باید بخش قابل توجه ای از واریانس( حداقل 50%) هر یک از نشانگرها را تبیین کند. همچنین همبستگی مطلق بین سازه و هر یک از متغیرهای آشکار( بارهای عاملی استاندارد شدۀ مطلق) باید از 7/0 بالاتر باشد. علاوه بر این، بعضی از روان سنج ها توصیه می کنند که اگر نشانگرهای انعکاسی، بارهای عاملی استاندارد شده شان کوچکتر از 4/0 باشد، آنها را از مدل اندازه گیری حذف کنیم. البته در صورتی که اعتبار نشانگر پایین است و حذف این نشانگر باعث افزایش قابل توجه اعتبار می شود باید نسبت به حذف این نشانگر اقدام کرد. برای ارزیابی روایی معمولاً دو نوع روایی فرعی بررسی می شود: روایی همگرا و روایی تشخیصی. روایی همگرا نشان می دهد که یک مجموعه از نشانگرها معرّف سازۀ زیربنایی یکسانی هستند که از طریق تک بعدی بودنشان نشان داده می شوند. فرنل و لارکر(1981) استفاده از میانگین واریانس استخراج شده را به عنوان معیاری از روایی همگرا پیشنهاد می کنند. میانگین واریانس استخراج شده حداقل 5/0 نشان دهندۀ روایی همگرای مناسب است. به این معنی که متغیر مکنون قادر است بیشتر از نصف واریانس نشانگرهایش را تبیین کند. روایی تشخیصی مفهوم مکمل روایی همگرا است و بدین منظور به کار می رود که آیا دو مفهوم متفاوت تفاوت کافی با هم دارند یا خیر. در مدل مسیرPLS دو اندازه گیری روایی تشخیصی مطرح می شود: معیار فرنل لارکر( میانگین واریانس استخراج شده) و وارسی بارها. در معیار فرنل-لارکر فرض بر این است که متغیر مکنون مورد نظر واریانس مشترک بیشتری با نشانگرهای تعیین شده نسبت به هر متغیر مکنون دیگری دارد. در اصطلاحات آماری جذر میانگین واریانس استخراج شده هر متغیر مکنون باید بیشتر از حداکثر همبستگی آن متغیر مکنون با متغیرهای مکنون دیگر باشد. دومین معیار روایی تشخیصی، معمولاً آزادانه تر است: بارهای هر کدام از نشانگرهای مورد نظر باید بیشتر از بارهای دیگر باشد. اگر چه معیار فرنل – لارکر روایی تشخیصی در سطح سازه است، وارسی بارها امکان این ارزیابی را در سطح نشانگرها فراهم می کند. علاوه بر این شاخص ها، شاخص اشتراک نیز امکان آزمون کلّی مدل اندازه گیری را فراهم می آورد که مقادیر مثبت این شاخص نشانگر کیفیت مناسب مدل اندازه گیری است.

جدول 3-3 ارزشیابی مدل اندازه گیری انعکاسی

در مجموع برای داشتن مدل اندازه گیری انعکاسی معتبر و پایا، باید به همۀ معیارهای جدول بالا توجه نمود. اگر یکی از این موارد برآورد نشود، محقق ممکن است بخواهد بعضی از نشانگرها را از مدل اندازه گیری حذف کند ویا در مدل مسیر، تجدید نظر کند.

آزمون مدل اندازه گیری ( مدل های تشکیل شونده)

بولن(1989) و باگوزی(1984) تأکید می کنند که ارزیابی اعتبار سنّتی و نظریه آزمون کلاسیک و مفاهیم اعتبار(یعنی همسانی درونی) و روایی سازه( یعنی؛ روایی همگرا و تشخیصی) با متغیرهای آشکار که در مدل های اندازه گیری تشکیل دهنده استفاده می شود، به کار نمی رود. این مفاهیم هنگامی که روش تشکیل دهنده به کار برده می شود بی معنی هستند. دیامانتوپولوس (2006) در رابطه با اندازه گیری های تشکیل دهنده، نتیجه گیری می کند که اعتبار، معیار نامربوطی برای ارزیابی کیفیت مدل اندازه گیری است. در این مدل ها اعتبار، اهمیت کمتری دارد؛ مهم آن است که روایی مطمئن باشد. برای بررسی روایی نشانگرهای تشکیل دهنده در مرحله اوّل از توجیه نظری و نظر کارشناس استفاده می شود. دومین مرحله برای ارزیابی روایی سازه های تشکیل دهنده، استفاده از تحلیل های آماری است که از دو سطح تشکیل شده اند: سطح سازه و سطح نشانگر. در سطح سازه، سؤالی که مطرح می شود این است که آیا شاخص های تشکیل دهنده حقیقتاً معنای مورد نظر را منتقل می کنند؟ اوّلین قسمت، بررسی اعتبار نومولوژیکال است: آیا نشانگرهای تشکیل دهنده در درون شبکه ای از فرضیه های مورد انتظار حرکت می کنند؟ روابط بین نشانگرهای تشکیل دهنده و دیگر سازه ها در مدل مسیر که بر اساس پژوهش های قبلی است، باید به اندازه کافی قوی و معنادار باشد. علاوه بر آن محققان باید به ضریب خطای سازه ها توجه داشته باشند، ضریب خطا معرّف بخشی از سازه است که به وسیله هیچ نشانگری تبیین نشده است. برای برآورد اندازه این خطا، می توان روایی بیرونی را به وسیله رگرسیون نشانگرهای تشکیل دهنده با استفاده از آزمون مدل انعکاسی همان سازه ارزیابی کرد. در ادبیات PLS هیچ آستانه ای برای روایی بیرونی پیشنهاد نشده است. اما هنسلر، رینگل و سینکویکس(2009) مقدار 8/0 را به عنوان حداقل روایی بیرونی پیشنهاد می کنند، به این معنی که نشانگر تشکیل دهنده حدود 80% از معنی داری سازۀ مورد نظر را تبیین می کند. در سطح نشانگر، این سؤال مطرح می شود که آیا هر کدام از نشانگرها سهمی در سازۀ تشکیل دهنده داسته و معنای مفهوم مورد نظر را منتقل می کنند؟ لازم است پژوهشگران برای بررسی اینکه آیا نشانگر خاصی باید در سازه وارد شود یا نه دو مورد را بررسی کنند. اوّلین مورد این است که یک نشانگر می تواند برای ساخت سازۀ تشکیل دهنده نامربوط باشد، زیرا اثر معناداری بر سازۀ تشکیل دهنده ندارد. دومین مورد این است که نشانگرها هم خطی چندگانه بالایی را نشان بدهند. این امر می تواند به این معنی باشد که اطلاعات نشانگرها زائد است. برای بررسی اوّلین مورد، معناداری برآورد وزن های نشانگر از طریق آزمون خودگردان سازی، بررسی شود. برای بررسی مورد دوم، پژوهشگران باید درجه هم خطی چندگانه میان نشانگرهای تشکیل دهنده را ارزیابی کنند. برای نمونه، با محاسبه عامل تورم واریانس یا ضرایب تحمل، باید این موضوع را بررسی نمایند. قانون کلّی اقتصادسنجی، توضیح می دهد که عامل تورم واریانس بیشتر از 10 سطح بحرانی از هم خطی چندگانه را آشکار می سازد. علاوه بر آن عامل تورم واریانس بیشتر از 1 هم خطی چندگانه را نشان می دهد و پژوهشگران باید مشکل هم خطی چندگانه را بر طرف کنند. گام ها و معیارهای متفاوت برای ارزیابی اعتبار شاخص های تشکیل دهنده در جدول 4-3 خلاصه شده است. در پایان، نشانگرهای تشکیل دهنده نباید به آسانی بر اساس نتایج آماری حذف شوند. چنین اقدامی ممکن است محتوای شاخص تشکیل دهنده را تغییر دهد. بنابراین، محقق باید هر دو نشانگرهای تشکیل دهنده معنادار و غیرمعنادار را در مدل اندازه گیری تا زمانی که توجیه نظری وجود دارد، نگه دارد. معمولاً مدل ساختاری PLS بعد از حذف نشانگرهای تشکیل دهنده غیرمعنادار یا دارای هم خطی چندگانه بالا، برآوردها را به سختی تغییر می دهد. این امر خود دلیلی برای نگهداری چنین نشانگرهایی در مدل مسیرPLS است. هم خطی چندگانه، می تواند برآورد وزن نشانگرها را تحریف کند.این واقعیت پژوهشگران را ملزم می کند تا هنگام تفسیر وزن های نشانگر به عنوان علامتی از اهمیت نشانگر حساس و آگاه باشند.

جدول 4-3 ارزیابی مدل اندازه گیری تشکیل دهنده

روابط نشانگرها-سازه

ماهیت روابط بین سازه ها و اندازه گیری هایشان به قواعد مطابقت اشاره دارد(با گوزی، 1984؛ فرنل، 1982) دو نوع اساسی از قواعد مطابقت وابسته به مدل یابی علّی وجود دارد:نشانگرهای انعکاسی و نشانگرهای تشکیل دهنده. در مورد اوّل، نشانگرها به عنوان انعکاس دهندۀ مشاهده نشده ها یا همان سازۀ زیربنایی در نظر گرفته می شوند و سازه، علّت نشانگرهای مشاهده نشده تلقی می شود. در این حالت یک سازه به وسیله ترکیب خطی نشانگرهایش تعیین می شود. در اینجا فرض آن است که همۀ نشانگرها انعکاسی هستند. در شرایطی که سازه های زیربنایی غیرقابل مشاهده به عنوان علّت نشانگرهای همخوان در نظر گرفته می شوند، روایی همگرا و اعتبار گویه موضوعیت می یابند. در مقابل، نشانگرهای تشکیل دهنده، علّت سازه هستند. در این صورت بررسی روایی و پایایی نشانگرهای تشکیل دهنده کاملاً ضروری نیست. در واقع، نشانگرهای تشکیل دهنده یک سازۀ یکسان می تواند مثبت، منفی یا بدون رابطه با یکدیگر باشند(بولن و لنونکس، 1991). در نتیجه، روابط مشاهده شدۀ میان نشانگرهای مرتبط با سازۀ مورد نظر،ممکن است معنادار نباشد.این امر به پژوهشگر اختیار تام برای انتخاب خودسرانه نوع مدل اندازه گیری را نمی دهد. به هر حال، کوهن و همکاران(1990) پیشنهاد می کنند هنگامی که رابطه تشکیل دهنده است، پژوهشگر باید بر اساس یک نظریه نیرومند که به شناخت نشانگرهای مناسب کمک می کند و نشانگرهای چندگانه( روایی محتوای قابل قبول) مدل اندازه گیری مورد نظر را طراحی کند. ممکن است انتخاب نوع نشانگرها(تشکیل دهنده یا انعکاسی) برای یک سازۀ خاص مشکل ساز باشد. پژوهشگر نیاز به تفکر دقیقی دارد تا درباره اینکه سازۀ زیربنایی به عنوان علّت اندازه گیری های مشاهده شده(رابطه های انعکاسی) هستند، یا اندازه گیری ها علّت سازه ها(رابطه های تشکیل دهنده) می باشند، تصمیم گیری کند. مثال برای مورد اوّل، عملکرد و برای مورد دوم، وضعیت های اجتماعی- اقتصادی می باشد. از دیدگاه آماری، استفاده از نشانگرهای تشکیل دهنده منجر به افزایش مقدار R² برای سازه های درون زا می شود( هر چند این اثر معمولاً زیاد نیست) و در نتیجه به حذف سازه های برون زا منتهی می شود، از این رو همۀ تبیین ها به سوی متغیرهای درون زا متمایل می شوند.

آزمون الگوی ساختاری مدل PLS

روایی و اعتبار برآوردهای مدل بیرونی اجازه ارزش یابی برآوردهای مدل مسیر درونی را می دهند. در جدول 5-3 معیارهایی که به وسیله آن مدل ساختاری ارزیابی می شوند، گزارش شده اند. معیار ضروری برای سنجش مدل ساختاری، ضریب تعیین( R²) متغیرهای مکنون درون زا است. چین(1998) مقادیر R²67/0،33/0و 19/0 در مدل مسیر PLS را به ترتیب قابل توجه، متوسط و ضعیف توصیف می کند. اگر سازه های مدل درونی خاصی متغیرهای مکنون درون زا را تنها با 1 یا 2 متغیر مکنون برون زا تبیین کنند، R² متوسط (33/0) قابل قبول است. اما اگر متغیرهای مکنون درون زا وابسته به چندین متغیر برون زا هستند، ارزش R² باید حداقل در سطح قابل توجه(67/0) باشد. ضرایب مسیر منفرد در مدل ساختاری PLS به عنوان ضرایب بتای استاندارد شدۀ رگرسیون OLS تفسیر می شوند. مسیرهای ساختاری، که علامت آنها مطابق با علامت جبری فرض شدۀ قبلی است، اعتبار تجربی جزئی از روابط مفروض نظری بین متغیرهای مکنون را تایید می کنند. مسیرهایی که علامت جبری بر خلاف انتظار دارند از فرض های پژوهشگر حمایت نمی کنند. به منظور تعیین معنی داری ضرایب مسیر و استنباط آماری؛ روش های نمونه گیری مجدد از قبیل برش متقاطع یا جک نایف و خودگردان سازی یا بوت استراپ باید استفاده شود.

برش متقاطع یا جک نایف: این روش با حذف تعداد خاصی واحد از نمونۀ اصلی(با اندازه N)، دوباره نمونه سازی می کند. این روش به صورت پیش فرض یک واحد را در هر زمان حذف می کند که باعث می شود هر زیر نمونۀ جک نایف در N-1 واحد در هر زمان تشکیل شود. افزایش تعداد واحدهای حذف شده باعث کاهش اساسی در نیرومندی آماره t می شود؛ زیرا باعث کاهش تعداد زیر نمونه ها می شود.

خود گردان سازی یا بوت استراپ: نمونه های بوت استراپ بر خلاف روش قبلی، از طریق نمونه گیری مجدد به روش جایگذاری از نمونۀ اصلی ساخته می شوند. این روش نمونه هایی به اندازه اصلی از روی همان نمونۀ اصلی می سازد. در روش PLS تعداد نمونه های مجدد را می توان تعیین کرد. مقدار پیش فرض آن 100 نمونه می باشد، اما تعداد بیشتر مانند 200 باعث دست یابی به برآورد خطای استاندارد منطقی تری می شود. بعضی از پژوهشگران تعداد 500 نمونه را نیز پیشنهاد کرده اند(تمه و دیگران،2006). روش بوت استراپ برای دست یابی یه خطاهای استاندارد یا مقادیر t معتبر نسبت به روش نمونه گیری مجدد قبلی یعنی جک نایف برتری دارد. اما مسئله اساسی که این روش با آن مواجه می باشد، این است که علامت متغیرهای مکنون با عدم تعیّن مواجه است. بنابراین تغییرات دلبخواهی و قراردادی در علامت، هنگام برآورد پارامترهای نمونه های بوت استراپ، می تواند باعث بالا رفتن خطای استاندارد آنها تا اندازه بحرانی و در نتیجه باعث پایین آمدن نسبت های t تا حد بحرانی شود. با توجه به این مسئله، روش های مختلفی برای اصلاح تغییر یا واژگونی علامت ایجاد شده است، که شامل تغییرات علامت فردی و تغییرات سطح سازه می باشند. در انتخاب اوّل(تغیرات علامت فردی) علامت وزن خارجی هر مورد یا فرد، مساوی با علامت آن در نمونۀ اصلی در نظر گرفته می شود. به خاطر اینکه این دستورالعمل به هم پیوستگی یا ارتباط کلّی مدل را بررسی نمی کند، به آن کد گذاری معکوس ذهنی نیز می گویند. بنابراین، از این روش باید با احتیاط استفاده شود. انتخاب دوم(تغیرات سطح سازه) بارهای هر متغیر مکنون را با بارهای نمونۀ اصلی مقایسه نموده و در صورتی که قدر مطلق جمع تفاوت بین بار اصلی و بوت استراپ بزرگتر از قدر مطلق جمع بارهای نمونۀ اصلی و بوت استراپ باشد، علامت وزن ها را معکوس می کند. اگرچه این دو روش تغییرات علامت را به صورت کاملاً درست تضمین نمی کنند، اما روش دوم بیشتر توصیه می شود( تمه و همکاران، 2006). ارزشیابی مهم دیگر، بررسی اثرات مستقیم و غیرمستقیم متغیر مکنون درون زا برای تحلیل واسطه ای و اثرات واسطه ای است. محققان با استفاده از مدل مسیر PLS نخست باید اثرات مستقیم مدل مسیر فرض شده را ارزیابی کنند و سپس با انجام تحلیل های اضافی در مورد اثرات واسطه ای تصمیم گیری کنند. ملاک دیگر ارزیابی مدل ساختاری توانایی مدل ها برای پیش بینی است. شاخص اندازه گیری روابط پیش بینی Q² استون-گیسر است که با استفاده از روش چشم بندی ارزیابی می شود. بر اساس ملاک استون-گیسر مدل باید نشانگرهای متغیر مکنون درون زا را پیش بینی کند. این روش ترکیبی از برازندگی تابع و وارسی اعتبار را نشان می دهد. با توجه به نظر والد(1983 صفحۀ 30 به نقل از تنن هاوس و همکاران، 2005) آزمون وارسی اعتبار استون و گیسر با مدل یابی نرم یا PLS یک پارچه و درهم تنیده است و شاخص نیرومندی برای بررسی مدل ساختاری به حساب می آید. بر اساس روش چشم بندی بخشی از داده های بلوک خاصی از نشانگرها در طول برآوردهای پارامتر حذف شده و سپس تلاش می شود تا با استفاده از پارامترهای برآورد شده، بخشی حذف شده برآورد شود. این روش تکرار می شود تا تمام نقاط داده ها حذف و برآورد شوند(تنن هاوس و همکاران،2005).

جدول 3-5 ارزیابی مدل ساختاری

برازش مدل PLS

لیزل و دیگر رویکردهای مدل یابی ساختاری مبتنی بر کوواریانس از طریق بازسازی دقیق ماتریس کوواریانس مشاهده شده به برآورد پارامتر می پردازند. در مقابل، هدف اوّلیه PLS کاهش خطا یا معادل آن، افزایش واریانس تبیین شده در همۀ سازه های درون زا است. میزان این واریانس در هر مدل PLS خاص، از طریق بررسی مقادیر R² سازه های درون زا تعیین می شود. یکی از تفاوت های اساسی بین لیزرل و PLS نامناسب بودن شاخص های موجود برای برازش مدل های برآورد شده با استفاده از PLS است. اگرچه در الگوریتم های PLS موجود آماره های برازندگی، از قبیل شاخص برازندگی هنجار شدۀ بنتلر و بونت را گزارش می کنند، اما آنها براساس این مفروضه بنا شده اند که پارامترهای مدل برآورد شده،برای کاهش تفاوت بین ماتریس های کوواریانس مشاهده شده و بازتولید شده می باشند، مفروضه ای که درPLS وجود ندارد. البته تنن هاوس و همکاران(2005) شاخص کلّی برازش را برای بررسی برازش مدل معرّفی نموده اند. ملاک کلّی برازش(GOF) را می توان با محاسبه میانگین هندسی میانگین اشتراک و R² به دست آورد.********************************** به باور تنن هاوس و همکاران(2005) شاخص GOF در مدل PLS راه حلّی عملی برای رفع مشکل بررسی برازش کلّی مدل بوده و همانند شاخص های برازش در روش های مبتنی بر کوواریانس عمل می کند و از آن می توان برای بررسی اعتبار با کیفیت مدل PLS به صورت کلّی استفاده کرد. این شاخص نیز همانند شاخص های برازش مدل لیزرل عمل می کند و بین صفر تا یک قرارداد و مقادیر نزدیک به یک نشانگر کیفیت مناسب مدل هستند(رینگل،2006).البته باید توجه داشت این شاخص بر خلاف شاخص های مبتنی برخی دو در مدل های لیزرل به بررسی میزان برازش مدل نظری با داده های گردآوری شده نمی پردازند، بلکه توانایی پیش بینی کلّی مدل را مورد بررسی قرار داده و نشان می دهد که مدل آزمون شده در پیش بینی متغیرهای مکنون درون زا موفق بوده است یا نه.

فصل چهارم: مقایسه مدل یابی معادلات ساختاری مبتنی بر کوواریانس و PLS

مقدمه

روش های مدل یابی معادلات ساختاری از قبیل لیزرل و کمترین مجذورات جزئی روش های تحلیل داده های نسل دوم هستند. این روش ها پژوهشگران را قادر می سازد تا به مجموعه ای از سؤالات تحقیقی وابسته به هم در یک تحلیل واحد، منظم و جامع از طریق مدل سازی روابط میان چندین سازۀ مستقل و وابسته، به صورت همزمان پاسخ دهند. این توانایی برای تحلیل همزمان، آن را از مدل های رگرسیون که می توانند تنها یک سطح از رابطۀ بین متغیرهای مستقل و وابسته در یک زمان را تحلیل کنند، متفاوت می سازد. برخلاف روش های رگرسیون، مدل یابی معادلات ساختاری علاوه بر ارزیابی مدل ساختاری، مدل اندازه گیری را نیز ارزشیابی می کند. تحلیل ترکیبی از اندازه گیری و مدل ساختاری اجازه می دهد، خطاهای اندازه گیری متغیرهای مشاهده شده به عنوان یک بخش انتگرال از مدل و ترکیب تحلیل عاملی با آزمون فرضیه ها، تحلیل شود.مدل یابی معادلات ساختاری مبتنی بر کوواریانس اشتقاق مرتبه دوم از قبیل تابع بیشینه درست نمایی را به کار می برد تا برآوردهای پارامتر را بیشینه سازد. PLS یک زنجیره مکرر از OLS و رگرسیون خطی چندگانه را به کار می برد. نسبت به برآورد واریانس همۀ متغیرهای مشاهده شده مانند مدل یابی معادلات ساختاری مبتنی بر کوواریانس، PLS پارامترها را به طوری که واریانس پس ماند را از همۀ متغیرهای وابسته در مدل کمینه سازد، برآورد می کند. تفاوت دیگر PLS و مدل یابی علّی مبتنی بر کوواریانس در نوع روابط آنها بین متغیرهای مشاهده شده و رابطه شان با سازه های مکنون است. PLS از دو نوع رابطۀ تشکیل دهنده و انعکاسی حمایت می کند. متغیرهای مشاهده شدۀ تشکیل دهنده علّت سازه-های مکنون هستند، یعنی ابعاد متفاوتی از آن را نشان می دهند. متغیرهای مشاهده شدۀ انعکاسی متغیر مکنون را منعکس می کنند و به عنوان معرّفی از سازه باید تک بعدی و مرتبط به هم باشند؛ در صورتی که مدل یابی معادلات ساختاری مبتنی بر کوواریانس تنها از متغیرهای مشاهده شدۀ انعکاسی حمایت می کند. از آنجایی که هدف مدل یابی مبتنی بر کوواریانس آزمون نظریه می باشد و زمانی آزمون نظریه نسبت به ساخت نظریه ارجحیت دارد، متغیرهای مشاهده شدۀ انعکاسی باید به تشکیل دهنده ترجیح داده شوند.

شاخص های آماری در مدل یابی معادلات ساختاری

در سطح مسیرها، مدل یابی معادلات ساختاری مبتنی بر کوواریانس بارهای گویه ها و خطای اندازه گیری با ارزش های t مربوط به خودشان را برآورد می کند. اعتبار سازه از طریق آلفای کرونباخ محاسبه می شود. مدل یابی معادلات ساختاری مبتنی بر کوواریانس همچنین ضرایب و ارزش های t روابط میان سازه های پنهان را نشان می دهد. ارزش های t باید معنادار باشد تا مسیرهای فرض شده را تأکید کند(بالای 96/1 یا 56/2، به ترتیب در سطح 05/0 و 010/0 معنی دار است). دومین آماره با برازندگی کلّی مدل مرتبط است. مهمترین این شاخص ها X² است. آماره X² همراه با P-Value باید غیرمعنادار باشد. زیرا X² غیر معنادار برازش خوب مدل را نشان می دهد. اما این ملاک به ندرت برآورده می شود، زیرا X² به حجم نمونه و قدرت آزمون بسیار حساس است. بنابراین به جای آن نسبت X² به درجه آزادی محاسبه می شود. برخی محققان پیشنهاد می کنند نسبت X² به درجه آزادی بین 1و2 باشد. در نهایت شاخص نکویی برازش، شاخص تعدیل شدۀ نکویی برازش و جذر پس ماندهای میانگین شاخص- هایی هستند که برای برازش کلّی مدل استفاده می شوند. شاخص نکویی برازش شاخص مطلقی است که مذل اندازه گیری و ساختاری را با داده ها ترکیب می کند. شاخص تعدیل شدۀ نکویی برازش این ارزش را با درجه آزادی در مدل تعدیل می کند. جذر پس ماندهای میانگین، واریانس پس ماند متغیرهای مشاهده شده و اینکه واریانس پس ماند یک متغیر چگونه با واریانس پس ماند گویه های دیگر همبسته است را محاسبه می کند.جذر پس ماندهای میانگین بزرگ برازش ضعیف مدل را نشان می دهد. PLS شاخص های آماری کمتری دارد. در سطح مدل اندازه گیری، PLS بارهای گویه ها وکوواریانس پس ماند را برآورد می کند. در سطح ساختاری، PLS ضرایب مسیر، همبستگی میان متغیرهای مکنون، واریانس تبیین شده و میانگین واریانس استخراج شدۀ متغیرهای مکنون را برآورد می کند. ارزش های t هر کدام از مسیرها و بارها با استفاده از روش برش متقاطع یا خودگردان سازی محاسبه می شود. برازش مناسب مدل براساس ضرایب مسیر معنادار، واریانس تبیین شده قابل قبول و همسانی درونی بالای 07/0 برای هر کدام از سازه ها محقق می شود. شاخص GOF نیز شاخصی برای بررسی برازش مدل جهت پیش بینی متغیرهای درون زا می باشد که مقادیر بیشتر از 9/0 نشانگر برازش مناسب مدل آزمون شده می باشد. اگر چه والد(1975) روش برآورد نقطه ثابت برای مدل یابی علّی به عنوان یک راه حل برای CBSEM توسعه داد، روش مدل یابی معادلات ساختاری مبنی بر برازندگی کوواریانس و رویکرد مبتنی بر واریانس کمترین مجذورات جزئی به جای رقیب بودن، مکمل یکدیگر هستند. مطابق با نظر جورسکاگ (1982) ML نظریه مدار است، و گذر از تحلیل اکتشافی به تحلیل تأییدی را مورد تأکید قرار می دهد. هدف PLS اصولاً تحلیل پیش بینی-علّی در موقعیت هایی با پیچیدگی بالا اما اطلاعات نظری ضعیف است. تمایز فلسفی بین این رویکردها این است که از CBSEM برای آزمون و توسعه نظریه و از PLS برای کاربردهای پیش بینی استفاده می کنند. همان گونه که در شکل 1-4 نشان داده شده است، در مدل یابی علّی مواقعی که نظریه قبلی نیرومند است و هدف بیشتر، آزمون و توسعه نظریه است، CBSEM روش آماری مناسب تری است، با این وجود، به علّت عدم تعیّن برآوردهای نمره عامل، دقت پیش بینی ضعیف تری دارد. البته این شرایط هنگام آزمون نظریه به خاطر اینکه روابط ساختاری میان مفاهیم اولویت دارد، جای نگرانی نیست.

شکل 1-4 هدف تحلیل پیش بینی

در موقعیت های پژوهشی که هدف آنها پیش بینی است و علاوه بر آن نظریه ضعیف بوده یا نیازی به فهم روابط زیربنایی نیست، شبکه های عصبی مصنوعی(ANN) ممکن است سودمند باشد. رویکرد شبکه های عصبی و بدون ایجاد یک مدل نظری معنادار. با این وجود هسو، چن و هسیه(2006) به این نتیجه رسیدند که روش مدل یابی معادلات ساختاری مبتنی بر شبکه های عصبی مصنوعی مشابه با مدل یابی مسیر PLS است. با استفاده از روش برآورد از سرگیری، رویکرد مدل یابی مسیر PLS نمره های متغیرهای مکنون را به عنوان ترکیب خطی دقیق از اندازه گیری های مشاهده شده محاسبه می کند. به موجب آن PLS از مشکل عدم تعیّن جلوگیری کرده و مقادیر دقیقی از نمره های مؤلفه فراهم می کند. رویکرد PLS برای کاربردهای مدل سازی علّی که هدفشان پیش بینی ویا ساخت نظریه می باشد مناسب است. اگر چه مدل یابی مسیر PLS می تواند برای تأیید نظریه نیز استفاده شود. در PLS برآوردهای پارامتر بر اساس توانایی برای کمینه ساختن واریانس های پس ماند متغیرهای وابسته یعنی هر دو متغیرهای مکنون مشاهده شده، به دست می آید. PLS با محاسبه خطای استاندارد برآوردها که از طریق برش متقاطع یا خود گردان سازی به دست می آید، ساختارهای مدل مسیر جزئی را ارزیابی می کند.عدم وجود تابع بهینه سازی کلّی و در نتیج اندازه گیری برازندگی کلّی مدل در PLS، استفاده از آن را برای آزمون نظریه محدود می کند. PLS به جای استفاده از مدل برای تبیین همپراشی میان همۀ متغیرها، که هدف CBSEM است، تبیین واریانس همۀ متغیرهای وابسته را بیشینه می سازد؛در نتیجه از اهداف پیش بینی مدارانه حمایت می کند.در واقع مدل یابی PLS به منظور بررسی میزان واریانس تبیین شده، یعنی بررسی معناداری رابطه ها ونتایج R شان طراحی شده است. اگرچه روش های مدل یابی مسیر CBSEM,PLS از دیدگاه آماری مفید هستند، برآوردهای PLS ممکن است معرّف های خوبی از نتایج CBSEM نشان دهند. اگر مقدمات CBSEM از قبیل فرض های توزیعی، کمینه ساختن حجم نمونه، یا بیشینه ساختن پیچیدگی مدل و موضوعات روش شناختی به وجود آمده از قبیل موارد هی وود، عدم توانایی در همگرایی راه حل، پارامترهایی که محدودیت های قابل قبول بیرونی و خطاهای استاندارد بزرگ مربوط به برآوردهای پارامتر دارند، موجود نباشند، PLS ممکن است روش معقولی برای آزمون نظریه باشد.زیرا کمترین مجذورات جزئی(PLS) از کمترین محدودیت بر نوع مقیاس های اندازه گیری، حجم نمونه و توزیع باقیمانده برخوردار است. در مدل یابی معادلات ساختاری مبتنی بر کوواریانس،

منبع:

عنوان: کتاب مدل معادلات ساختاری با PLS

نویسندگان : محمد عباس‌زاده و جواد امانی

ناشر : دانشگاه ارومیه

نوع فایل: کاغذی و چاپی

زبانک فارسی

تعداد صفحات : ۲۲۶ صفحه

‫5/5 ‫(2 نظر)

Sign up for Newsletter

انجام خدمات نرم افزار SMART PLS4

آموزش

مشاوره

انجام تحلیل

تعدادی از ویژگی های موجود در SmartPLS 4

آموزش Smart PLS4

More videos on SmartPLS 4

01

Crafted by hand

02

Passionate for real

03

We promote integrity

Explore our services

Branding

Interior design

Architecture